1016 . Your Ways
Description
You live in a small well-planned rectangular town in Phuket. The size of the central area of the
town is H kilometers * W kilometers. The central area is divided into HW unit blocks, each of
size 1 x 1 km2
. There are H + 1 streets going in the West to East direction, and there are W + 1
avenue going in the North-South direction. The central area can be seen as a rectangle on the
plane, as shown below.
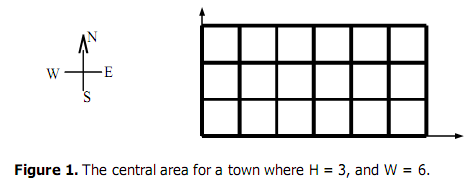
We can identify each intersection by its co-ordinate on the plane. For example, on the Figure
above the bottom-left corner is intersection (0,0), and the top-right corner is intersection (6,3).
Your house is at the bottom-left corner (i.e., intersection (0,0)) and you want to go to the
university at the top-right corner (i.e., intersection (W,H)). More over, you only want to go to
the university with wasting any efforts; therefore, you only want to walk from West-to-
East and South-to-North directions. Walking this way, in the example above there are 84
ways to reach the university.
You want to go to the university for K days. Things get more complicated when each morning,
the city blocks parts of streets and avenues to do some cleaning. The blocking is done in such a
way that it is not possible to reach parts of the streets or avenues which is blocked from some
other part which is blocked as well through any paths containing only West-to-East and South-
to-North walks.
You still want to go to the university using the same West-to-East and South-to-North
strategy. You want to find out for each day, how many ways you can reach the university by
only walking West-to-East and South-to-North. Since the number can be very big, we only want
the result modulo 2552.
Input Format
The first line contains an integer T, the number of test cases (1 <= T <= 5). Each test case is in
the following format.
The first line of each test case contains 3 integers: W, H, and K (1 <= W <= 1,000;
1 <= H <= 1,000; 1 <= K <= 10,000). W and H specify the size of the central area. K denotes the
number of days you want to go to the university.
The next K lines describe the information on broken parts of streets and avenues. More
specifically, line 1 + i, for 1 <= i <= K, starts with an integer Qi (1 <= Qi <= 100) denoting the
number of parts which are blocked. Then Qi sets of 4 integers describing the blocked parts
follow. Each part is described with 4 integers, A, B, C, and D (0 <= A <= C <= W; 0 <= B <= D <= H)
meaning that the parts connecting intersection (A,B) and (C,D) is blocked. It is guaranteed that
that part is a valid part of the streets or avenues, also C - A <= 1, and D - B <= 1, i.e., the part is
1 km long.
Output Format
For each test case, for each day, your program must output the number of ways to go to the
university modulo 2552 on a separate line. i.e., the output for each test case must contains K
lines.
Sample Input 1
2 2 2 3 1 0 0 0 1 2 1 0 2 0 0 2 1 2 1 1 1 2 1 100 150 2 1 99 150 100 150 2 99 150 100 150 100 149 100 150
Sample Output 1
3 4 4 1562 0
Hints
The amount of I/O for this task is quite large. Therefore, when reading input, you should avoid using
java.io.Scanner which is much slower than using java.io.BufferedReader.
Problem Source
Migrated from old NTUJ.
2009Phuket
Subtasks
| No. | Testdata Range | Score |
|---|