1017 . Hexagonal Sticks
Description
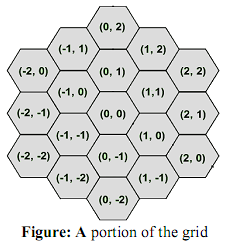
In this problem, we will consider an infinite hexagonal grid. The grid consists of equal regular
hexagonal cells arranged in the fashion shown below. The figure also elucidates the coordinate
system used to identify each cell. Each cell of the grid can be empty or blocked.
There are few sticks placed randomly on this grid. The length of each stick is one ‘hexagonal
unit’. This means, the end points of a stick lies on the centers of neighboring cells. Your job is to
move the sticks so that a closed regular hexagonal figure is formed.
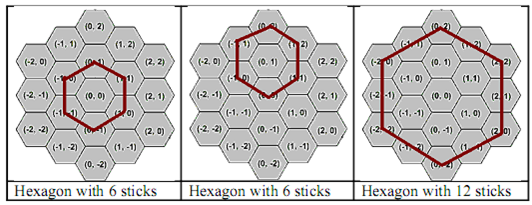
The diagrams below show some closed hexagonal figures made of sticks.
You will be given the initial coordinates of the sticks that are placed on the grid. You will also be
given the coordinates of the cells that are blocked. In each move you can do one of the
followings:
- Select one stick and throw it out
- Select one stick and rotate it 60 degrees clockwise/anti-clockwise about one of the end points
- Select one stick and push it along the length of the stick.
The sticks can never occupy a cell that is blocked. However, two sticks can occupy the same
cells at the same time.
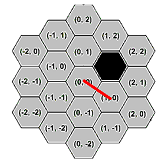
Consider the scenario shown above. We have an obstacle situated at coordinate (1, 1) and a stick
at coordinate (0, 0) -> (1, 0). The four possible moves that can be made are depicted below
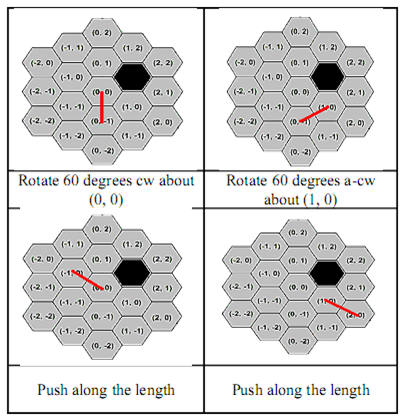
After all the moves are made, you have to ensure a closed regular hexagonal shape is formed
with no other sticks lying around. This means the grid should contain exactly 6*x sticks where x
is positive integer. Can you do this in minimum number of moves?
Input Format
The first line of input is an integer T(T<50) that indicates the number of test cases. Each case
starts with a non-negative integer S(S<9) that gives you the number of sticks available. The next
S lines give you the coordinates of the sticks. The coordinates of the sticks will be of the format
x1 y1 x2 y2, which means there is a stick from (x1, y1) to (x2, y2). The coordinates will be valid
and the length of each stick will be one hexagonal unit as mentioned above. The next line will
give you a non-negative integer B(B<20) that indicates the number of obstacles. Each of the next
B lines will give you the coordinates of the obstacles. The coordinate will be of the format x1 y1.
It is guaranteed that the given blocks will not overlap with any given sticks. All the coordinates
(sticks and blocks) will have values in the range [-4, 4].
Note: Remember that we are dealing with infinite grids. So in the optimal result, it could be
possible that the hexagonal sticks lie outside [-4, 4].
Output Format
For each case, output the case number first followed by the minimum number of moves required.
If it is impossible to form a hexagonal grid, output “impossible” instead. Adhere to the sample
input/output for exact format.
Sample Input 1
3 6 -1 -1 -1 0 -1 0 0 1 0 1 1 1 1 1 1 0 1 0 0 -1 0 -1 -1 -1 0 5 -1 0 0 1 0 1 1 1 1 1 1 0 1 0 0 -1 0 -1 -1 -1 0 7 -2 -2 -2 -1 -1 -1 -1 0 0 0 1 1 0 0 1 1 0 0 1 1 1 1 2 2 1 2 2 2 2 1 0 2 0
Sample Output 1
Case 1: 0 Case 2: impossible Case 3: 9
Hints
Problem Source
Migrated from old NTUJ.
2009Phuket
Subtasks
| No. | Testdata Range | Score |
|---|