1019 . Synnerg Lifeform
Description
In a science laboratory, scientists found a new kind of tiny lifeforms and named them
“synnergs”. Until now, few knowledge about synnergs are known. Some of these knowledge are
as follow.
There are more than one types of synnerg.- Any new born synnerg have the same lifetime.
- Two synnergs (of certain types) can extend their lifetimes by unifying themselves
together which will also transform them into a new target synnerg. The lifetime of
this new target is the summation of both sources' lifetimes multiplied with an
amplification factor. The type of this new target may vary from its sources. From
many experiments, scientists found a set of rules to describe the unification of each
synnerg pair . Some of these rules can be shown as the following table.

When scientists arrange two or more of new born synnergs into a sequence, each
synnerg in this sequence will try to unify itself with the one on its left or its right (and
make the sequence shorter). This unification process will continue again and again
(recursively). There might be lots of possible ways to unify an input sequence which
also affect the lifetime of each unified synnerg.
For example of unification steps, please see the following table.
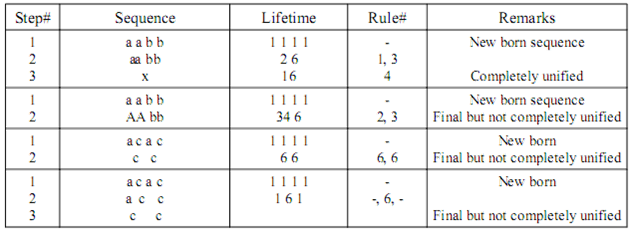
In the first example, at the first step there is a sequence of 4 new born synnergs “a a b b” where
their lifetimes are “1 1 1 1” respectively. In the second step, these synnergs unify themselves into
a sequence of two synnergs “aa[a a] bb[b b]” (using rule no.1 and 3) where aa's lifetime is
2=(1+1)*1 and bb's lifetime is 6=(1+1)*3. In the third step, “aa bb” unify themselves into “xaa
bb where its lifetime is 16=(6+2)*2.
In the second example, at the first step, the beginning sequence is the same sequence in the first
example. But they alternatively unify themselves into “AA[a a] bb[b b]” (using rule no.2 and 3
instead) where their lifetimes are 34=(1+1)*17 and 6(1+1)*3 respectively. This sequence is also
the final sequence which means that it is unable to unify furthermore but it is not a completely
unified sequence. However, this alternative final sequence has longer life time comparing to the
final sequence in the first example.
The third and fourth example also show the alternative ways of unifying the sequence “a c a c”.
Please be notify that each rule is not sensitive to the order of its sources.
Goal
The scientists would like you to create a program that can find all highest lifetime synnergs that
can be created by unifying a given sequence of newborn synnergs. The solution may not always
be the one that is completely unified. Only part or sub-sequence unification is also acceptable.
Input Format
Input is a standard input which contains 2 parts of data which are separated by a blank line.
The first part is a set of unification rules.
- Each line in this first part contains one of unification rule.
- Each rule consists of 4 fields separated by spaces.
- The first 3 fields are target, source #1 and source #2 respectively. Each fields is a synnerg
name which is represented by a string of at most 20 alpha-numeric characters. - The last field is the amplification factor which is a positive integer less than or equal to
100.
The second part is a set of input sequences of synnergs.
- Each line in this second part contains one input sequence of synnergs.
- Each input sequence is a sequence of synnergs separated by spaces.
The blank line after the second part is the termination of the input.
Output Format
For each sequence of input, write 2 parts of output as follows
- In the first line, write the total of number of highest synnergs followed by a space and
then the maximum lifetime of these synnergs. - In the following lines, write each of the solutions in each line. Each solution contains 3
fields separated by spaces. These fields are a synnerg, its starting and finishing offset. If
there are two or more solutions, they must be sorted by ascending order. The priority of
comparison in sorting is the 2nd
field, the 3rd
field and the 1st
field (or the starting offset,
the finishing offset and the synnerg). For comparisons in sorting, the 2nd
and 3rd
field
comparison is based on numerical values, and the 1st
field is based on
alphabetical/lexicographical (ASCII) order.
Sample Input 1
aa a a 1 AA a a 17 bb b b 3 x aa bb 2 x x a 2 c c a 3 a a b b a a b b a a a b b a a a c a c a c
Sample Output 1
1 34 AA 1 2 2 34 AA 1 2 x 1 5 1 70 x 1 6 1 6 c 1 2 1 21 c 1 3
Hints
There are 6 rules and 5 input sequences in this sample input.
For the first case, even though there is a completed unification “x[aa[a a] bb[b b]]” (starting from 1
to 4), its lifetime is only 16 (= {(1+1)*1 + (1+1)*3}*2) times of a newborn, which is less than 34 of
“AA[a a]” starting from 1 to 2.
For the second case, there are 2 solutions. The first is “AA” starting from 1 to 2. The second is “x”
starting from 1 to 5.
For the third case, there is only one solution. “x” now is the only winner (with 70 points).
For the fourth and the fifth cases, (parts of) the results has been unified according to the last rule.
Since each rule is not sensitive to the order of its sources, any rule is applicable if both of its source
are found. (“c c a 3” equals “c a c 3”.)
Problem Source
Migrated from old NTUJ.
2009Phuket
Subtasks
| No. | Testdata Range | Score |
|---|