1029 . Heroes Arrangement
Description
There are N heroes in the Kingdom of Heroes, each hero has a special range
of activity, this “range” is a delta-shaped region (triangle region including
the boundary; it is guaranteed that all triangles will neither degenerate into
a segment nor a point in the King’s angle of view), and heroes can appear in any
point in his activity range. The king, standing at the Origin (0, 0, 0), is observing
the heroes. No range of activity will contain the king’s position.
You may assume that no hero could meet others, that means these “range” have
no common point. Your task is to find number K, indicating that the king can choose
at most K heroes such that no pairs of chosen heroes cause one may block the king’s
view line to observe another. In other words, no hero can appear on the segment
between another hero and the King.
Input Format
There are multiple test cases, the number of them, T, is given in the very
first line of the input, followed by T cases.
For each test case:
First line contains an integer N, the number of heroes, 1≤N≤40. Then N lines
follow, each line contains nine integers x1 y1 z1 x2 y2 z2 x3 y3 z3, denoting
the coordinates of the delta-shaped regions’ vertex respectively, -100≤x1, y1, z1, x2, y2, z2, x3, y3, z3≤100.
Output Format
Output a single line with a number K with case number, the maximum number of
heroes that king can choose.
Sample Input 1
2 2 0 0 1 1 2 1 -1 2 1 0 0 2 1 -2 2 -1 -2 2 2 0 0 1 1 2 1 -1 2 1 0 0 -1 1 -2 -1 -1 -2 -1
Sample Output 1
Case #1: 1 Case #2: 2
Hints
The sample image of the sample input is drawn below, the small sphere is the
position of the king.
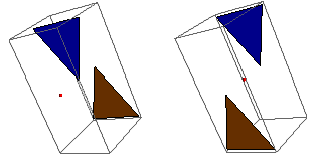
Problem Source
Migrated from old NTUJ.
2009Shanghai
Subtasks
| No. | Testdata Range | Score |
|---|