103 . Hangover
Description
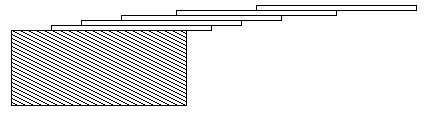
How far can you make a stack of cards overhang a table? If you have
one card, you can create a maximum overhang of half a card length.
(We're assuming that the cards must be perpendicular to the table.) With
two cards you can make the top card overhang the bottom one by half a
card length, and the bottom one overhang the table by a third of a card
length, for a total maximum overhang of 1/2 + 1/3 =
5/6 card lengths. In general you can make n cards overhang by 1/2
+ 1/3 + 1/4 + ... + 1/(n
+ 1) card lengths, where the top card overhangs the second by
1/2, the second overhangs tha third by 1/3, the third overhangs the
fourth by 1/4, etc., and the bottom card overhangs the table by
1/(n + 1). This is illustrated in the figure below.
Input Format
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
Output Format
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
Sample Input 1
1.00 3.71 0.04 5.19 0.00
Sample Output 1
3 card(s) 61 card(s) 1 card(s) 273 card(s)
Hints
Problem Source
Migrated from old NTUJ.
Subtasks
| No. | Testdata Range | Score |
|---|