1030 . Island Explorer
Description
A group of explorers has found a solitary island. They land on the island and
explore it along a straight line. They build a lot of campsites while they advance.
So the campsites are laid on the line.
Coincidently, another group of explorers land on the island at the same time.
They also build several campsites along another straight line. Now the explorers
meet at the island and they decide to connect all the campsites with telegraph
line so that they can communicate with each other wherever they are.
Simply building segments that connect a campsite to another is quite easy,
but the telegraph line is rare. So they decide to connect all the campsites with
as less telegraph line as possible. Two campsites are connected if they are directly
connected with telegraph line or they are both connected to another campsite.
Input Format
There are multiple test cases.
The number of the test cases is in the first line of the input.
For each test case, first line contains two integers N and M (0≤N, M≤10000),
which N is the number of the campsites of the first group of explorers and M is
the number of the campsites of the second group of explorers. And there exist
at least one campsite.
The next two lines contain eight integers Ax, Ay, Bx, By, Cx, Cy, Dx, Dy. Their
absolute values are less than 1000. The integers are the coordinates of four points
A, B, C and D. The exploring path of the first group is begin with the first point
A and end with the second point B, and the path of the second group is from the
third point C to the fourth point D. Every pair of points is distinct.
The last two lines of the test case contain N and M real numbers; they indicate
the positions of the campsites. Suppose the i-th real number in the first line
is t. It means the x-coordinate of the i-th campsite is Ax * t + Bx * (1-t), and
the y-coordinate is Ay * t + By * (1-t). Equally, the campsite on the second straight
line is C * t + D * (1-t). You can assume that there are at most four digits in
the decimal part, and the numbers are always between 0 and 1 inclusive.
Output Format
For each test case, output contains only a real number rounded to 0.001.
Sample Input 1
1 4 4 0 0 10 10 0 10 10 0 0.1 0.3 0.6 0.8 0.1 0.3 0.6 0.8
Sample Output 1
Case #1: 19.638
Hints
總之就是 %.3lf 或 setprecision(3)
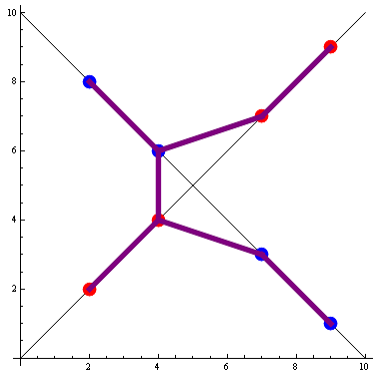
The graph below shows the solution of the sample test
Problem Source
Migrated from old NTUJ.
2009Shanghai
Subtasks
| No. | Testdata Range | Score |
|---|