ICPC (International Connecting Points Company) starts to sell a new railway toy. It consists
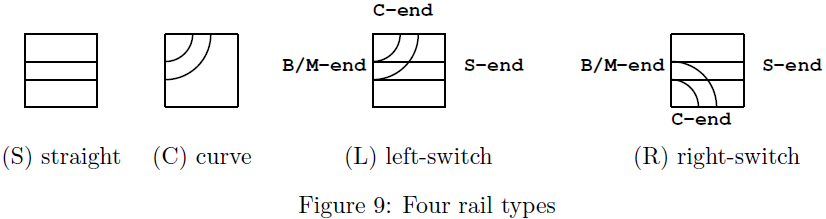
of a toy tramcar and many rail units on square frames of the same size. There are four types
of rail units, namely, straight (S), curve (C), left-switch (L) and right-switch (R) as shown in
Figure 9. A switch has three ends, namely, branch/merge-end (B/M-end), straight-end (S-end)
and curve-end (C-end).

A switch is either in “through” or “branching” state. When the tramcar comes from B/M-end,
and if the switch is in the through-state, the tramcar goes through to S-end and the state changes
to branching; if the switch is in the branching-state, it branches toward C-end and the state
changes to through. When the tramcar comes from S-end or C-end, it goes out from B/M-end
regardless of the state. The state does not change in this case.

Kids are given rail units of various types that fill a rectangle area of w × h, as shown in Figure
10(a). Rail units meeting at an edge of adjacent two frames are automatically connected.
Each rail unit may be independently rotated around the center of its frame by multiples of 90
degrees in order to change the connection of rail units, but its position cannot be changed.

Kids should make “valid” layouts by rotating each rail unit, such as getting Figure 10(b) from
Figure 10(a). A layout is valid when all rails at three ends of every switch are directly or
indirectly connected to an end of another switch or itself. A layout in Figure 10(c) is invalid as
well as Figure 10(a). Invalid layouts are frowned upon.

When a tramcar runs in a valid layout, it will eventually begin to repeat the same route forever.
That is, we will eventually find the tramcar periodically comes to the same running condition,
which is a triple of the tramcar position in the rectangle area, its direction, and the set of the
states of all the switches.

A periodical route is a sequence of rail units on which the tramcar starts from a rail unit with
a running condition and returns to the same rail unit with the same running condition for the first time. A periodical route through a switch or switches is called the “fun route”, since kids
like the rattling sound the tramcar makes when it passes through a switch. The tramcar takes
the same unit time to go through a rail unit, not depending on the types of the unit or the
tramcar directions. After the tramcar starts on a rail unit on a “fun route”, it will come back to
the same unit with the same running condition, sooner or later. The fun time T of a fun route
is the number of time units that the tramcar takes for going around the route.

Of course, kids better enjoy layouts with longer fun time. Given a variety of rail units placed
on a rectangular area, your job is to rotate the given rail units appropriately and to find the fun
route with the longest fun time in the valid layouts.

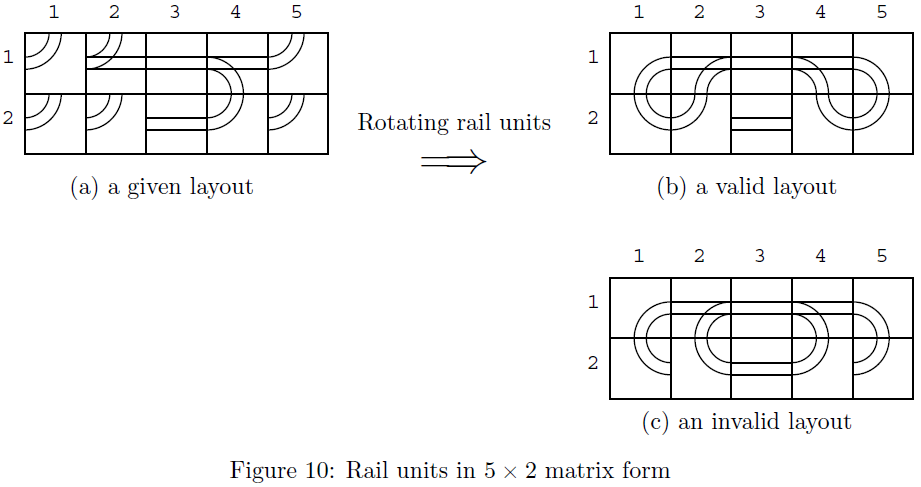
For example, there is a fun route in Figure 10(b). Its fun time is 24. Let the toy tramcar start
from B/M-end at (1, 2) toward (1, 3) and the states of all the switches are the through-states. It
goes through (1, 3), (1, 4), (1, 5), (2, 5), (2, 4), (1, 4), (1, 3), (1, 2), (1, 1), (2, 1), (2, 2) and (1, 2).
Here, the tramcar goes through (1, 2) with the same position and the same direction, but with
the different states of the switches. Then the tramcar goes through (1, 3), (1, 4), (2, 4), (2, 5),
(1, 5), (1, 4), (1, 3), (1, 2), (2, 2), (2, 1), (1, 1) and (1, 2). Here, the tramcar goes through (1, 2)
again, but with the same switch states as the initial ones. Counting the rail units the tramcar
visited, the tramcar should have run 24 units of time after its start, and thus the fun time is 24.

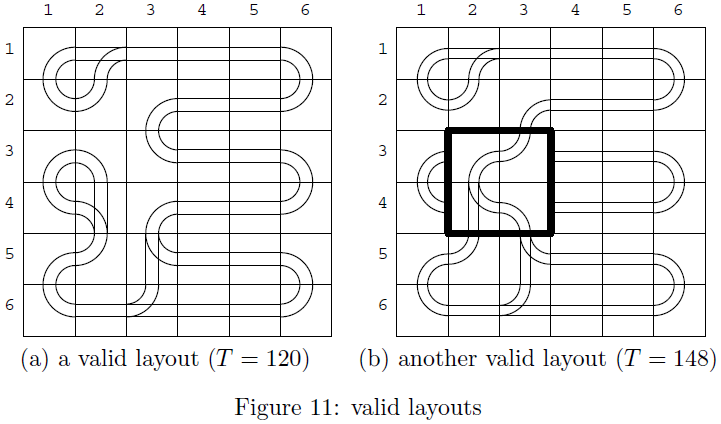
There may be many valid layouts with the given rail units. For example, a valid layout containing
a fun route with the fun time 120 is shown in Figure 11(a). Another valid layout containing a
fun route with the fun time 148 derived from that in Figure 11(a) is shown in Figure 11(b). The
four rail units whose rotations are changed from Figure 11(a) are indicated by the thick lines.

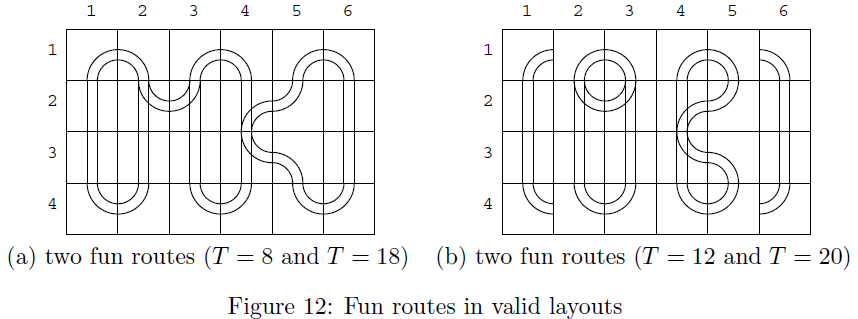
A valid layout depicted in Figure 12(a) contains two fun routes, where one consists of the rail
units (1, 1), (2, 1), (3, 1), (4, 1), (4, 2), (3, 2), (2, 2), (1, 2) with T = 8, and the other consists of
all the remaining rail units with T = 18.

Another valid layout depicted in Figure 12(b) has two fun routes whose fun times are T = 12
and T = 20. The layout in Figure 12(a) is different from that in Figure 12(b) at the eight rail
units rotated by multiples of 90 degrees. There are other valid layouts with some rotations of
rail units but there is no fun route with the fun time longer than 20, so that the longest fun
time for this example (Figure 12) is 20.

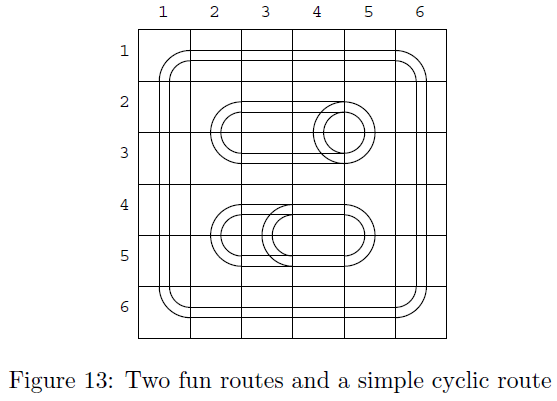
Note that there may be simple cyclic routes that do not go through any switches in a valid
layout, which are not counted as the fun routes. In Figure 13, there are two fun routes and one
simple cyclic route. Their fun times are 12 and 14, respectively. The required time for going
around the simple cyclic route is 20 that is greater than fun times of the fun routes. However,
the longest fun time is still 14.