1059 . The Legend of ICPC
Description
In the exciting adventure game "The Legend of ICPC", characters have different attributes such as the ability to solve DP, creativity, speed of eating snacks, dota... etc. Characters in the game are of obtain "skillpoint" by solving different problems, then each skillpoint can be spend into specific attributes, increasing the attribute by one with each skillpoint spent. Spent skillpoint could not be taken back, i.e. they become attributes and the process cannot be reversed. Also, you must spend integral skillpoint on an attribute, i.e. you are not allowed to put 1.7 skillpoints into your intellegence...etc
Given the attributes, we could draw a characteristic graph by taking each attribute as axis and marking the corresponding value on the axis, then connecting all points to form a polygon. Things should be illustrated clearly as in the figure below:
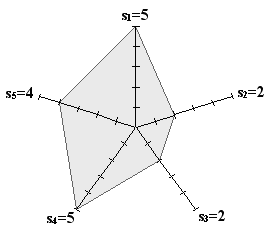
this is an example of a character with 5 different attribute, each having a value of 5, 2, 2, 5, 4 respectively.
The "strength" of a character is equal to the area of the polygon formed in its characteristic graph.
Now kelvin is a character in the game. Given the attributes of kelvin currently, and his available skill points at disposal, determine the maximum strength kelvin could achieve after spending all the skillpoints, and tell him how much stronger could he be.
Input Format
There are multiple input in the testcase. The input is ended by EOF.
Each testcase begin with an n and k indicating the number of different skills, and number of available skillpoints. Then follows n integers being the value of each attributes. The values are given in order, that is, if plotted in the characteristic graph they are given in a clockwise sense.
You can assume the initial area of the polygon formed is nonzero.
Output Format
For each testcase, output a floating number X on a single line indicating that Kelvin could become stronger by a factor of X, if he spend all his skillpoints wisely.
Sample Input 1
6 4 2 2 2 3 1 3
Sample Output 1
1.923076
Hints
This series of homework are all problems with ungiven input size! It is (at least the original aim of it is) to enable us to acutally think about a problem from scratch, without the "additional informations" implicated by a specific given problem size.
Of course, we do hope it'd be a rather fun experience, since in real life problems often we do not know whether a problem exhibits an efficient algorithm or is even solvable!!
Anyway, the input size, though not specified, will be "reasonable". That is, if the optimal algorithm is O(n3), then n would be something like 300, if O(nlgn), then perhaps 200000.. etc. Also if values are not otherwise specified, they could be expected to be for example, int.
Info: 本題輸出為浮點數,絕對或相對誤差 1e-5 以下視為正確
Problem Source
Migrated from old NTUJ.
kelvin
Subtasks
| No. | Testdata Range | Score |
|---|