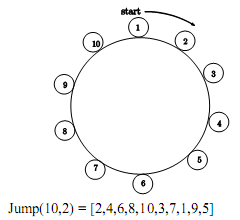
Integers 1,2,3, …, n are placed on a circle in the increasing order as in the following figure. We want to
construct a sequence from these numbers on a circle. Starting with the number 1, we continually go round by
picking out each k-th number and send to a sequence queue until all numbers on the circle are exhausted. This
linearly arranged numbers in the queue are called Jump(n,k) sequence where 1 ≤ n, k.

Let us compute Jump(10,2) sequence. The first 5 picked numbers are 2, 4, 6, 8, 10 as shown in the following
figure. And 3, 7, 1, 9 and 5 will follow. So we get Jump(10,2) = [2,4,6,8,10,3,7,1,9,5]. In a similar way,
we can get easily Jump(13,3) = [3,6,9,12,2,7,11,4,10,5,1,8,13], Jump(13,10) = [10,7,5,4,6,9,13,8,3,12,1,11,2]
and Jump(10, 19)=[9,10,3,8,1,6,4,5,7,2].

You write a program to print out the last three numbers of Jump(n,k) for n, k given. For example suppose that

n=10, k=2, then you should print 1, 9 and 5 on the output file. Note that Jump(1,k)=[1].