1093 . Bear
Description
The Infinite city is divided into unitary square blocks by an infinite number of south-north and
west-east two-way streets. One of the south-north streets is labeled 0, and the street numbers
increase to the east and decrease to west. Similarly, one of the west-east streets is labeled 0,
and the numbers increase to the north and decrease to the south.
Every intersection is labeled by an ordered pair of numbers of the streets that intersect (the
first being the number of south-north street). Some street sections are more important and are
called main streets.
One day sheriff Wolf (the fiercest caretaker of the Infinite city) is patrolling the streets and at
intersection (A,B) he notices a car with a few members of the well-known BEAR gang. Wolf
has heard of the BEARs’ plans to break into the city’s Honey Warehouse, which is located near
the intersection (0, 0), and decides to stop them.
However, they haven’t commited any crime so far and Wolf can’t arrest them. But he has the
authority to stop his car at any intersection and block exactly one of the four unit segments that
meet at this intersection. However he can’t block a unit segment that belongs to a main street.
SoWolf decides to pursue the BEARs and just before they reach an intersection, he may overtake
their car and block one of the four unit segments at the intersection. The BEARs will be able to
drive into the intersection, but they won’t be able to exit the intersection to a segment blocked
by the sheriff’s car.
The sheriff wants to keep the BEARs as far away from the Honey Warehouse as possible. Find
the maximum distance D, such that any intersection (x, y) the BEARs may reach satisfies the
condition max(|x|, |y|) >= D.
Input Format
The first line of each input testcase contains two integers: A and B (|A| <= 106, |B| <= 106),
the starting point of the BEARs. The second line contains one integer N (0 <= N <= 500), the
number of main streets. Each of the following N lines contains four integers: X1, Y1, X2, Y2
(|Xi| <= 106, |Yi| <= 106), meaning that the street section between intersections (X1, Y1) and
(X2, Y2) is a main street. Either X1 = X2 or Y1 = Y2 holds.
Note: input containts multiple testcase.
Output Format
The only line of output must contain the maximum value of D.
Sample Input 1
3 3 3 1 0 3 0 0 0 0 3 3 0 3 1 3 3 3 1 0 3 0 0 0 0 3 3 0 3 1
Sample Output 1
1 1
Hints
The following figure illustrates how the BEARs can get to within distance 1 of the warehouse:
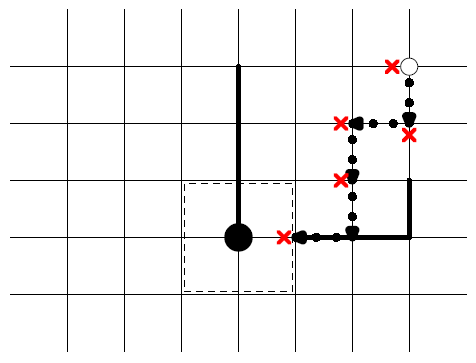
Even though the BEARs may continue trying forever, the sheriff can prevent them from ever
getting closer to the warehouse.
Problem Source
Migrated from old NTUJ.
BOI 2010
Subtasks
| No. | Testdata Range | Score |
|---|