1159 . Equilateral Dominoes
Description
We've all seen regular dominoes before-they look like rectangular tiles, twice as long as they are wide, with pips designating a number between 1 and 6 on each of their two ends. The object of a dominoes game involves some variation of tiling the dominoes so that the numbers on adjacent dominoes match up.
Now what if we were to make the dominoes out of equilateral triangles, like this:
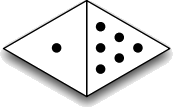
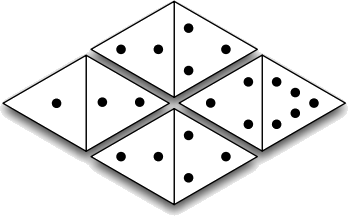
Input Format
The input consists of multiple test cases.
The first line of each test case contains an integer N, 1<= N<=6,
the number of equilateral dominoes in that set.
This is followed by N lines with two integers each (values between 1 and 6 inclusive), with each line indicating the pip values on each of the dominoes in the set.
Input is followed by a single line with N = 0, which should not be processed.
Output Format
For each test case, output a single line containing the highest tiling score that can be achieved with the given
set of equilateral dominoes. If there is no valid tiling of the dominoes, output a zero.
Sample Input 1
4 1 2 2 3 3 2 4 3 2 5 6 2 1 4 3 2 3 4 1 5 1 6 0
Sample Output 1
4 0 1
Hints
Problem Source
Migrated from old NTUJ.
2010 Stanford Local Round 1
Subtasks
| No. | Testdata Range | Score |
|---|