1173 . around the tracK
Description
After The Stig's identity was revealed, the TV
show Top Gear is in dire need of a new, tame
racing driver to replace him. And of course
you have been asked to take the job. However,
you are not very fond of driving quickly, and
especially not around the twisting and turning
tracks they use in the show. To help you
alleviate this problem, one of your algorithmic
friends has suggested that you should calculate
the roundtrip with the least possible amount of
turning required.
The driving track consists of unique, straight lines, and there are always exactly 2 or 4
roads heading out from each node. A roundtrip must be an Eulerian circuit, i.e. it must
traverse each edge of the graph exactly once, and end up where it started. (Such a circuit
is guaranteed to exist in the input graphs.) Thus the total amount of turning is the sum
of the turning required at each node, where continuing in a straight line means a turn of
0. The roads on the track can be driven in any direction.
Input Format
There are multiple test cases in the input file. For each test case:
One line with 3 <= N <= 10000 -- the number of nodes -- and N <= M <= 2N -- the number of edges.
N lines with the x and y coordinates of each node, in order. 0 <= x, y <= 10000. The nodes
have unique coordinate pairs.
M lines with two space separated numbers i and j, denoting an edge between nodes i and
j. The nodes are 0-indexed.
Output Format
The least amount of turning you must do to complete an Eulerian circuit, in radians.
Sample Input 1
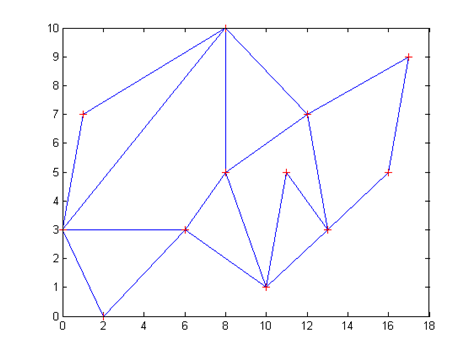
3 3 0 0 0 1 1 0 0 1 0 2 1 2 12 19 2 0 0 3 1 7 8 10 8 5 6 3 10 1 11 5 13 3 12 7 16 5 17 9 0 1 0 5 1 5 1 2 1 3 2 3 3 4 3 9 4 5 4 9 4 6 5 6 6 7 6 8 7 8 8 9 8 10 9 11 10 11
Sample Output 1
6.283185 22.428486
Hints
Info: 本題輸出為浮點數,絕對或相對誤差 1e-6 以下視為正確
Problem Source
Migrated from old NTUJ.
Nordic Collegiate Programming Contest 2010
Subtasks
| No. | Testdata Range | Score |
|---|