1306 . Polygon
Description
A simple polygon with N vertices is drawn on an infinite rectangular grid. For such a polygon, only
neighboring edges touch at their common vertex; no other of its edges intersect or touch. All vertices
of the polygon lie on grid points, i.e., vertices have integer coordinates.
Your task is to find the total length of grid line segments which lie strictly inside the given polygon
(these line segments are highlighted in the drawings below).
Input Format
The first line of input contains a single integer N, the number of vertices of the polygon. Each of the
following N lines contains two integers x and y, the coordinates of one vertex. The vertices are given
either in clockwise or counterclockwise order. All vertices are distinct, but more than two consecutive
vertices may lie on a line.
3 ≦ N ≦ 100000
-500000000 ≦ x, y ≦ 500000000
Output Format
The only line of output must contain a decimal number: the total length of grid line segments which
lie strictly inside the given polygon.
Sample Input 1
3 5 1 2 4 1 1 5 0 0 -2 2 -2 -1 2 -2 2 0
Sample Output 1
10.0 12.5
Hints
For the first sample,
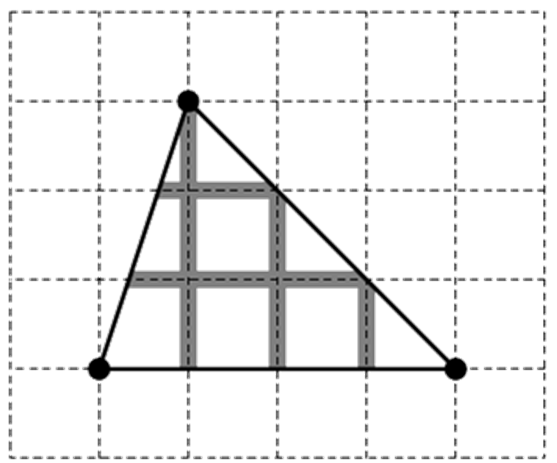
The length of horizontal lines is 4/3 + 8/3 = 4. The length of vertical lines is 3 + 2 + 1 = 6.
The total length is 4 + 6 = 10.
For the second sample,
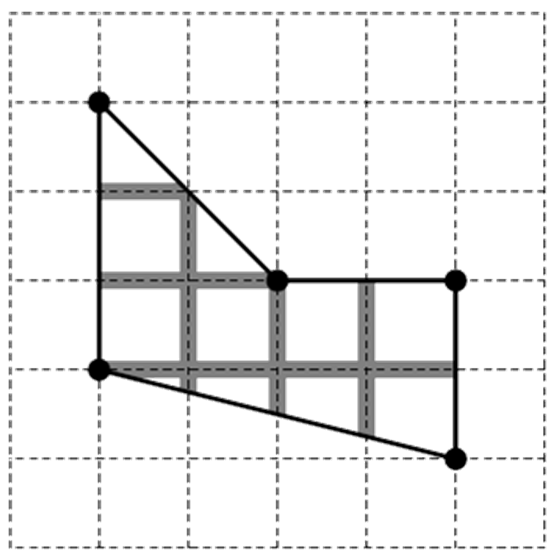
The length of horizontal lines is 1 + 2 + 4 = 7. The length of vertical lines is 9/4 + 3/2 + 7/4 = 5.5.
The total length is 7 + 5.5 = 12.5.
Info: 本題輸出為浮點數,絕對或相對誤差 1e-6 以下視為正確
Problem Source
Migrated from old NTUJ.
BOI2011 Competition day 2
Subtasks
| No. | Testdata Range | Score |
|---|
