1307 . Tree Mirroring
Description
Let T be a rooted tree (a connected undirected acylic graph), and let S be a perfect copy of T.
Construct a new graph by taking the union of T and S, and merging the corresponding leaf nodes (but
never the root). We call such a graph a tree-mirrored graph.
Write a program that determines if an arbitrary undirected connected graph is a tree-mirrored graph.
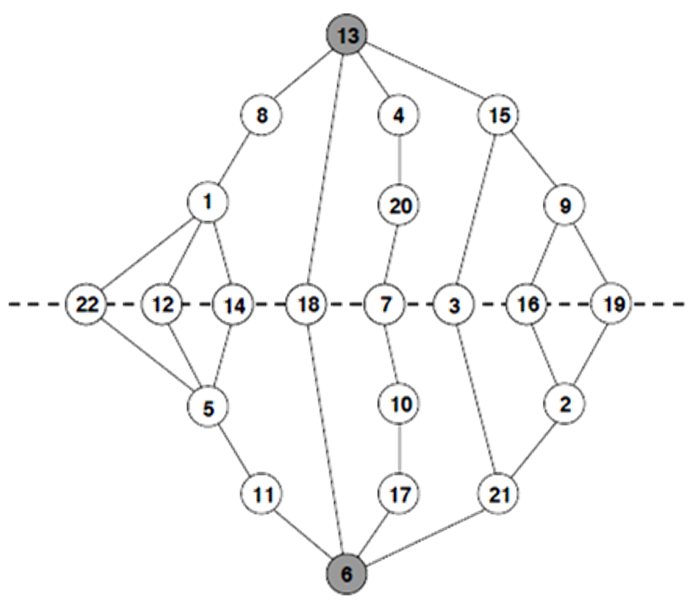
Figure 1: An example of a tree-mirrored graph. The figure corresponds to the third example test case.
Input Format
The first line of input contains two integers N and M, the number of vertices and edges of a graph G.
The vertices in G are labeled from 1 to N. The following M lines describe the edges. Each such line
contains two integers x and y (x ≠ y; 1 ≦ x, y ≦ N), describing one edge. There will be at most one
edge between any pair of vertices.
3 ≦ N, M ≦ 100000
Output Format
The first and only line of output should contain the string YES if the graph G is a tree-mirrored graph,
and NO otherwise.
Sample Input 1
7 7 1 2 2 3 3 4 4 5 5 6 6 7 7 1 6 6 1 2 2 3 2 4 3 5 4 5 5 6
Sample Output 1
NO YES
Hints
Problem Source
Migrated from old NTUJ.
BOI2011 Competition day 2
Subtasks
| No. | Testdata Range | Score |
|---|