1323 . Game of Rope
TopCoder
Description
Peter collects many rubber-bands.
He collects so many of them, that sometimes he wonders why does he collects so many rubber-bands in the first place!
Therefore one day, a wonderful idea striked him and Peter invented the following single-player game:
Suppose Peter has a rectangular board, with thin poles sticking out from each gridpoint. One should be able to imagine that, a rubber-band could be strapped around the poles and enclosing a certain shape. There are also several 'X's marked on the board, and the "edges" of the board have varying costs. The goal of the game, thus, is to enclose all the 'X's using limited rubber-bands, while using minimum costs.
Here however, the outline formed by the rubber-band must be only horizontal or vertical. See the figure below for reference.
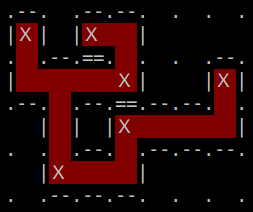 |
 |
As stated above, each "edge" (connecting two gridpoints) has a cost. The "cost" of a specific enclosure of rubber-band is simply the sum of costs of all edges that it uses.
Now Peter have K rubberbands, using at most K rubber-bands (not necessarily all), what is the minimum cost for him to enclose all the 'X's ?
Note that the following important rules must be obeyed, though.
Rules:
|
1. must not include a point that is not used. So the following configuration is forbidden.

|
|
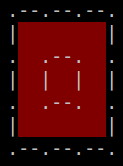
2. A "hole" formed by the outer side of rubber-band does not count. (For example in the figure below, the middle cell is considered "outside" the rubber-band)

|
|
3. Even using two rubber bands will not form a donut (so the arrangement below is illegal by rule 1, as the outer-rope contains four unused grid-points)
|
|
4. A rubber-band is NOT allowed to cross itself, and the enclosed area (the red part) has to be connected. Two different rubber-bands, however, could cross each other. Sharing edges on the same rubber-band is also permitted. (so the arrangement below is illegal)

|
|
5. An edge that is used multiple time is also count multiple time in cost
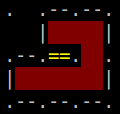
|
Input Format
The first line is an integer T, indicating the number of testcases.
Each testcase first consists of R, C being the grid's height and width, then a number K being the number of ropes Peter has, and N being the number of Xs. Then follows:
- N lines of pairs of integers being the position of the X's. Rows and Columns are numbered from top/left starting from 0 (to R-1 and C-1, respectively).
- R+1 lines of C integers being the cost of each horizontal edges, from top row to bottom row, and in each row from left to right.
- R lines of C+1 integers being the cost of each vertical edges, from top row to bottom row, and in each row from left to right.
1 <= T <= 50
1 <= K <= 15
1 <= Number of 'X's <= 10
1 <= Length of grid <= 15
100 <= cost of an edge <= 300 (so the sample graph above is actually not a valid cost distribution)
Output Format
For each testcase, output a single number being the minimum cost to envelope all Xs.
Sample Input 1
2 9 4 3 9 0 2 1 2 2 2 4 0 4 3 5 0 5 1 6 1 7 3 300 300 100 100 300 300 100 300 300 300 100 300 300 300 100 100 100 300 300 100 300 100 300 100 100 300 300 300 300 300 300 100 300 300 100 300 300 100 100 100 300 300 100 300 100 300 300 100 300 100 300 300 100 300 100 300 300 300 300 300 100 100 300 100 100 100 300 100 300 300 300 100 100 300 300 300 100 100 100 100 300 100 300 300 100 4 7 2 6 0 0 0 2 1 3 1 6 2 3 3 1 230 210 240 150 140 280 130 190 200 100 300 220 250 190 280 190 170 300 150 300 290 200 210 240 140 150 260 270 210 130 100 200 200 230 100 200 300 280 130 110 230 200 110 100 200 300 220 200 140 220 230 100 230 270 280 120 300 300 220 200 100 160 200 300 300 110 140
Sample Output 1
3800 4420
Hints
Problem Source
Migrated from old NTUJ.
kelvin
Subtasks
| No. | Testdata Range | Score |
|---|