1370 . Spread Out Message
Description
Wakkas is a great chief of a tribe. As a leader, every day he has to deal with many jobs. Once he makes a decision, the message must be sent to all of his people. Traditionally, Wakkas announces a message in a square and simply let the message be spread out among people. Sometimes, not all people are notified of a message by this way. If a person is not in the square during the announcement of a message, it is possible that no one tells him the message. Even though he hears the message, he may doubt the credibility if the message is sent by a stranger.
Another problem is that one person might hear the same message over and over again. Thus, some people do not spread out any message since they are bored to do so.
Recently, Wakkas figures out a more efficient way to spread out a message. He maintains a list, called the spreading list, which consists of pairs of persons. Each pair (pi , pj ) of the list indicates that pi needs to tell pj any new message he received and pj also needs to tell pi any new message he received. For example, assume that there are four persons p1 , p2 , p3 , and p4 and ((p2 , p3 ), (p1 , p3 ), (p3 , p4 )) is the spreading list. If Wakkas tells a new message to p1 ; p1 in turn tells the message to p3 ; and finally, p3 tells the message to both p2 and p4 . (See Figure 1.)
To announce a new message, Wakkas always tells the message only to p1 .
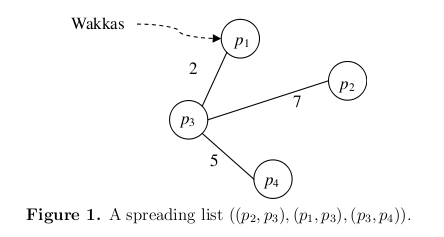
Wakkas wants the length of the spreading list to be as short as possible. After some study, he finds that a list of n − 1 pairs is necessary and sufficient for all people to receive a new message, where n is the number of his people. Wakkas also wants that a new message can be received by all of his people as soon as possible. To do so, for every pair (pi , pj ) of his people, he assigns a score f(i,j) according to the degree of familiarity between pi and pj , where a higher score indicates that the two people are more familiar with each other. Wakkas defines the score of a spreading list as the total score of its pairs. For example, if f(2,3) = 7, f(1,3) = 2, and f(3,4) = 5, the score of the spreading list in Figure 1 is 14. Wakkas believes that the higher the score of a spreading list, the shorter the time required for all people to receive a new message.
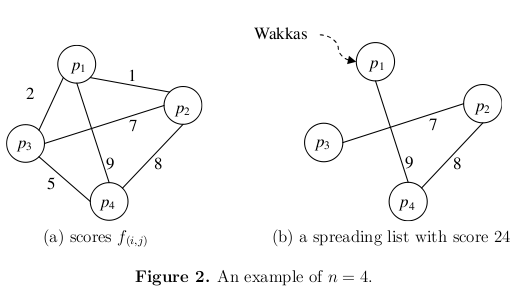
Wakkas’ target is to create a spreading list of highest score. The created spreading list
must contain exactly n − 1 pairs which are sufficient for all people to receive a new message. Consider the example in Figure 2(a). Figure 2(b) shows a spreading list with the highest score 24. Wakkas is too busy to handle it; therefore, he seeks for your help.
Input Format
There are at most 100 test cases. Each test case describes the tribe in two parts. The first part is a single integer n, where 2 ≤ n ≤ 100. The second part consists of n lines indicating the scores among the n people. The ith line contains n integers f(i,1) , f(i,2) , ..., f(i,n) . Note that f(i,j) = f(j,i) for 1 ≤ i, j ≤ n, and f(i,i) = 0 for 1 ≤ i ≤ n.
The last test case will be followed by a line consisting of an integer 0.
Technical Specification
1. The number of people in the tribe, n : 2 ≤ n ≤ 100.
2. The score, f(i,j) : 0 ≤ f(i,j) ≤ 100.
Output Format
For each test case, print a line containing the highest score of a spreading list.
Sample Input 1
3 0 5 2 5 0 3 2 3 0 4 0 1 2 9 1 0 7 8 2 7 0 5 9 8 5 0 0
Sample Output 1
8 24
Hints
Problem Source
Migrated from old NTUJ.
The ACM-ICPC 2010 Asia Regional Contest, Site Kaohsiung
Subtasks
| No. | Testdata Range | Score |
|---|