Nintendo Game Company develops a game played on a two-dimensional square lattice (2D-lattice). A 2D-lattice can be viewed as a graph with vertex set V = {[a, b]| a, b ∈ Z}. The vertices are
represented as ordered pairs and two vertices are adjacent if and only if the corresponding squares share
a side of lattice. Figure 1 illustrates a 2D-lattice. Given a sequence of length m over the symbols 0 and
1, the conformations of the sequence are restricted to self-avoiding paths embedded in a 2D-lattice,
where a self-avoiding path is a path in a 2D-lattice that does not visit the same vertex more than once.
The detailed description of the game is as follows.

    Let p = p₁ ... p_m be a sequence of length m over symbols 0 and 1, and let = (V, E) be a
2D-lattice. An embedding of p into is an injective function φ : {1,...,m} → V from the positions of the sequence to the vertices of the lattice that assigns adjacent positions in p to adjacent vertices in , i.e., (φ(i), φ(i + 1)) ∈ E for all 1 ≤ i ≤ m − 1. These edges (φ(i), φ(i + 1)) ∈ E for 1 ≤ i ≤ m − 1 are called binding edges. An embedding of p into is called a conformation. An edge (x, y) of is called contact edge if it is not a binding edge, but there exist i, j ∈ {1,...,m} such that φ(i) = x, φ(j) = y,
and p_i = p_j = 1.

    The score of a conformation φ equals the number of the contact edges in . Figure 2 illustrates a conformation with score 7. An optimal conformation of a sequence in is a conformation that
maximizes the number of contact edges. Given a sequence, a player is asked to find an optimal conformation and your task is to write a computer program to compute the score of an optimal conformation.

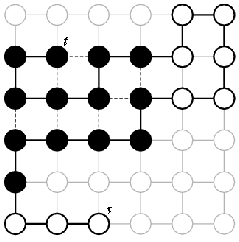
Figure 2: A conformation of the sequence 0001111110000001111111, where “ • ” represents 1,
“ ◦ ” represents 0, the bold edges represent the binding edges, and the dotted edges represent the
contact edges. The score of this conformation equals 7. In addition, s and t are the beginning
0 and the ending 1 of the sequence.