1375 . Houses
Description
We want to build houses on a rectangular filed. The size of the field is m by n units. Here m denotes the number of columns and n denotes the number of rows. The size of a houses is 1 by 2 units,
or 2 by 1 units. Each house occupies two adjacent unit squares and the houses cannot overlap. In
addition, there are k unit squares in the field that are not sutiable for building, so you cannot build
houses on them. We will call these squares bad squares. Given the size of the filed, the locations of bad
squares, please compute the maximum number of houses that can be built in the field.
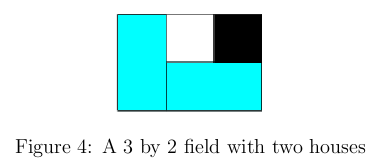
Let the location of the bottom left square be (0, 0). The following figure shows a 3 by 2 field with
a bad square at location (2, 1), and we can build at most two houses in this field.
Input Format
The input file contains a set of test cases, and two test cases are separated by a blank line. Each
test case consists of two parts. The first part has one line continaing the size of the field m and n
(1 ≤ m, n ≤ 200), and the number of bad squares k. The second part has k lines. Each line has two
indices x and y indicating the location of a bad square, where 0 ≤ x < m and 0 ≤ y < n. We assume
that when m, n, and k is 0 then it indicates the end of test cases.
Output Format
The output for each test case is a line that has the maximum number of houses that could be built for
this test case.
Sample Input 1
3 2 1 2 1 0 0 0
Sample Output 1
2
Hints
Problem Source
Migrated from old NTUJ.
The ACM-ICPC 2010 Asia Regional Contest, Site Kaohsiung
Subtasks
| No. | Testdata Range | Score |
|---|