1379 . Falling Gift Game
Description
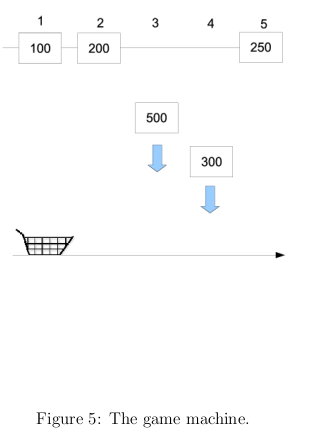
There are falling gifts from a game machine. Each gift is labeled with a price (see Fig. 1). The
gifts fall at different timing which people do not know. The game allows you to move a cart at the
floor of the game machine to collect the gifts from left to right using a control button (starting from
line 1). When you press the button, the cart will move right. Moving from a line to it next line will
take 1 second. You cannot move backward. Of course, you can wait at a line to guarantee a catch.
There is no need to move the car to the end of right before the game ends.
In a strange occasion, you got the falling timing setting of the machine. Let the game start at 0
second. By calculating how much time it takes to fall, you exactly know when a gift will hit the floor
of the game machine. You are a greedy man and decide to come up a great plan to get the maximum
value from the machine.
Input Format
In each test case, the first line is the number of gifts G (G < 500). If G is 0 it means the end of input
data. Next, there are G lines of gift information. The gift information is listed from left to right. Each
gift information is described by time t and price p. The value of t, 1 ≤ t ≤ 2G, is the time the gift will
hit the floor of the game machine. Every gift will fall to the floor within 2G seconds. The value of p is
the price of the gift, which is a positive integer, 1 ≤ p ≤ 10000. For example, t = 3 and p = 100 mean
the gift will reach the floor at the 3-rd second when the game starts and the price will be 100.
Output Format
Please output the maximum value you can collect in a game.
Sample Input 1
5 5 100 4 200 3 500 4 300 4 250 3 5 500 3 300 4 300 5 2 200 4 200 5 200 3 500 7 50 0
Sample Output 1
800 600 650
Hints
Problem Source
Migrated from old NTUJ.
The ACM-ICPC 2010 Asia Regional Contest, Site Kaohsiung
Subtasks
| No. | Testdata Range | Score |
|---|