1413 . RB-Tree
Description
A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically to implement associative arrays. It is complex, but has good worst-case running time for its operations and is efficient in practice: it can search, insert, and delete in O(log n) time, where n is total number of elements in the tree.
A red–black tree is a binary search tree where each node has a color attribute, the value of which is either red or black. In addition to the ordinary requirements imposed on binary search trees, the following requirements apply to red–black trees:
1. A node is either red or black.
2. The root is black.
3. All leaves are black ( The leaves mentioned in this problem are those NIL nodes).
4. Both children of every red node are black.
5. Every simple path from a given node to any of its descendant leaves contains the same number of black nodes.
In this problem, you will read in a tree, and please calculate how many ways you can color this tree to make it become a red-black tree.
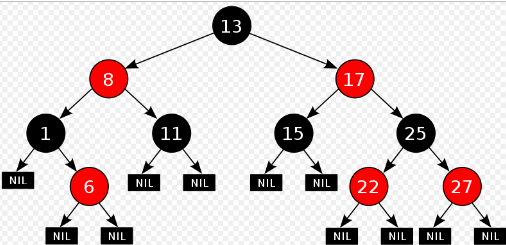
Input Format
There may be multiple test cases, terminated by EOF.
The first line of each test case consists of one positive integer N, denoting how many nodes of this tree. Following N-1 lines, each will contains two integers , P and S, means P is the father of S. And for all inputs will satisfy 1<=N<=31, -100<=P, S<=100. The test data guarantee the tree is a binary tree, and any of two nodes have different value. Notice that all NIL leaves will never in the input and won't be counted in N( because all leaves are black, it's no need to consider them.)
The first sample input is correspond to the figure above.
Output Format
Output a single integer denoting how many ways you can color this tree to make it become a red-black tree. If it can't be a red-black tree, output 0
Sample Input 1
10 1 6 8 11 8 1 17 15 13 17 13 8 17 25 25 22 25 27 1
Sample Output 1
3 1
Hints
Problem Source
Migrated from old NTUJ.
Subtasks
| No. | Testdata Range | Score |
|---|