1437 . Delightful Teleport
TopCoder
Description
In the year 3012, a teleport machine has been invented.
It can transport a person from a transmitter to the corresponding receiver,
even if the transmitter and the receiver are on different planets.
The most rich farmer, John, owns many planets as his farms.
However, he didn't have enough money to buy teleport machines to let him teleport from every planet to every other planet.
Therefor he designed some rules to build the teleport machines:
- His home can teleport to every planet that he owns.
- If the number of cows on planet A is more than that on planet B, then
John can teleport from A to B if and only if GCD(number of cows on A, number of cows on B) is greater than the number K. - If the number of cows on planet A is equal to that on planet B, then
John can teleport between A and B freely.
\item If the number of cows on planet A is less than that on planet B, then
John can teleport from A to B if and only if GCD(number of cows on A, number of cows on B) is less than or equal to the number K.
Here is an example. The arrows stand for the directions that John can teleport along.
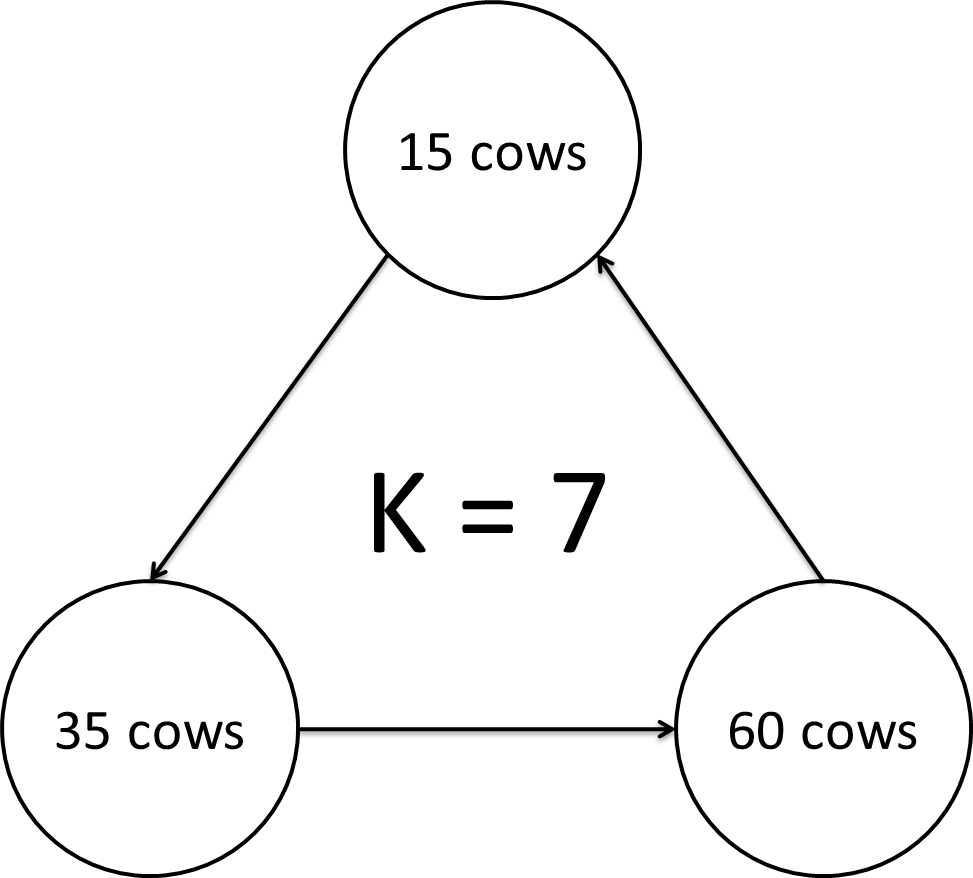
One day, John's favorite cow, Mary, gets lost.
John knows that Mary must be in one of his planets, and he wants to go to every planet to find her.
Nevertheless, John wants to spend least time on teleporting, so he comes to you.
Could you find out the longest path that does not arrive any planet more than once?
Warn: 本題有 specialjudge
Input Format
There are many parallel universes, so there are many test cases.
The actual number of test cases T is shown in the first line of the input.
Each test case contains two lines.
The first line of each test case has two integers N and K,
where N is the number of planets that farmer John owns and K is the teleport control number (see above).
The second line contains N integers, a1,...,aN, describing the number of cows in each planet.
1<=T<=50, 1<=N<=100000, 1<=K<=20, 1<=ai<231.
Output Format
For each test case, please output two lines.
The first line contains an integer M, indicating the length of the longest path.
The second line contains M integers, describe the longest teleport path that does not arrive any planet twice.
Please use the number of cows to denote a planet.
If there are more then one longest path, you can output any of them.
Sample Input 1
2 2 1 2 4 3 7 15 35 60
Sample Output 1
2 4 2 3 15 35 60
Hints
Problem Source
Migrated from old NTUJ.
a127
Subtasks
| No. | Testdata Range | Score |
|---|