1439 . Fence IV
TopCoder
Description
The fences come back again!
However, this time we face a new kind of fences: curved fence.
A curved fence is a part of a circle, which can be defined by two coordinates (x1,y1), (x2,y2) and an angle θ.
(See figure for more details.)
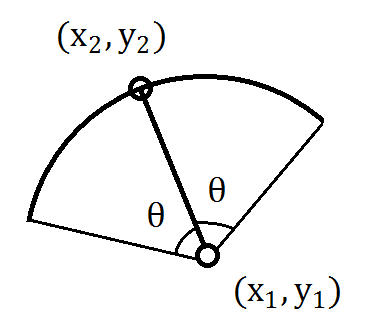
There are already many curved fences settled on the field.
To prevent the fences from being destroyed by the coming typhoon, we are going to nail on every intersection of two fences to strengthen them.
The question is: How many intersections are there on the field?
Note that the fences never overlap, nor "touch" each others at the end.
Input Format
There are several cases in the input file.
The first line of the input file contains an integer T<=10 specifying the number of cases.
Each case starts with N, the number of curved fences, N<=1000.
The following N lines describe the fences.
A fence is expressed by five floating point numbers 0<=x1, y1, x2, y2<=10000 and 0<=θ<=π, where θ is measured in radian.
Output Format
For each case, output the number of intersections in a line.
Sample Input 1
1 2 0 1 0 2 3 1 0 2 0 3
Sample Output 1
1
Hints
Problem Source
Migrated from old NTUJ.
pP
Subtasks
| No. | Testdata Range | Score |
|---|