1447 . Awkward Lights
Description
You are working as a night watchman in an office building. Your task is to check whether all
the lights in the building are turned off after all the office workers in the building have left the
office. If there are lights that are turned on, you must turn off those lights. This task is not as
easy as it sounds to be because of the strange behavior of the lighting system of the building as
described below. Although an electrical engineer checked the lighting system carefully, he could
not determine the cause of this behavior. So you have no option but to continue to rely on this
system for the time being.
Each floor in the building consists of a grid of square rooms. Every room is equipped with
one light and one toggle switch. A toggle switch has two positions but they do not mean fixed
ON/OFF. When the position of the toggle switch of a room is changed to the other position,
in addition to that room, the ON/OFF states of the lights of the rooms at a certain Manhattan
distance from that room are reversed. The Manhattan distance between the room at (x1, y1) of
a grid of rooms and the room at (x2, y2) is given by |x1 − x2| + |y1 − y2|. For example, if the
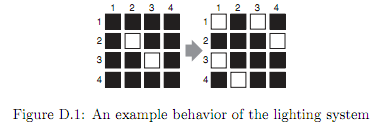
position of the toggle switch of the room at (2, 2) of a 4 × 4 grid of rooms is changed and the
given Manhattan distance is two, the ON/OFF states of the lights of the rooms at (1, 1), (1, 3),
(2, 4), (3, 1), (3, 3), and (4, 2) as well as at (2, 2) are reversed as shown in Figure D.1, where
black and white squares represent the ON/OFF states of the lights.
Your mission is to write a program that answer whether all the lights on a floor can be turned
off.
Input Format
The input is a sequence of datasets. Each dataset is formatted as follows.
m n d
S11 S12 S13 ... S1m
S21 S22 S23 ... S2m
...
Sn1 Sn2 Sn3 ... Snm
The first line of a dataset contains three integers. m and n (1 ≤ m ≤ 25, 1 ≤ n ≤ 25) are
the numbers of columns and rows of the grid, respectively. d (1 ≤ d ≤ m + n) indicates the
Manhattan distance. Subsequent n lines of m integers are the initial ON/OFF states. Each Sij
(1 ≤ i ≤ n, 1 ≤ j ≤ m) indicates the initial ON/OFF state of the light of the room at (i, j): ‘0’
for OFF and ‘1’ for ON.
The end of the input is indicated by a line containing three zeros.
Output Format
For each dataset, output ‘1’ if all the lights can be turned off. If not, output ‘0’. In either case,
print it in one line for each input dataset.
Sample Input 1
1 1 1 1 2 2 1 1 1 1 1 3 2 1 1 0 1 0 1 0 3 3 1 1 0 1 0 1 0 1 0 1 4 4 2 1 1 0 1 0 0 0 1 1 0 1 1 1 0 0 0 5 5 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 5 5 2 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 11 11 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11 11 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13 13 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Sample Output 1
1 1 0 1 0 0 1 1 0 1
Hints
Problem Source
Migrated from old NTUJ.
ACM ICPC 2010 Japan site
Subtasks
| No. | Testdata Range | Score |
|---|