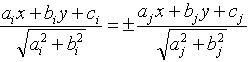1465 . Bisectors
Description
We all probably know how to find equation
of bisectors in Coordinate Geometry. If the equations of two lines are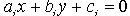 
and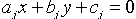 
, then the equations of the bisectors of the four angles they create are given by 
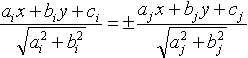and . Now one has to be quite intelligent to find out for which
angles to choose the ‘+’(plus) sign and for which angles to choose the
‘-’(minus) sign. You will have to do similar sort of choosing in this problem.
Suppose there is a fixed point (Cx, Cy) and there are n
(n≤10000) other points around it. No two points from these n points are
collinear with (Cx, Cy). If you connect all these point
with (Cx, Cy) you will get a star-topology like image
made of n lines. The equations of these n lines are also given and only these
equations must be used when finding the equation of bisectors. This n lines
create n(n-1)/2 acute or obtuse angles in total and so they have total n(n-1)/2
bisectors. You have to find out how many of these bisectors have equations
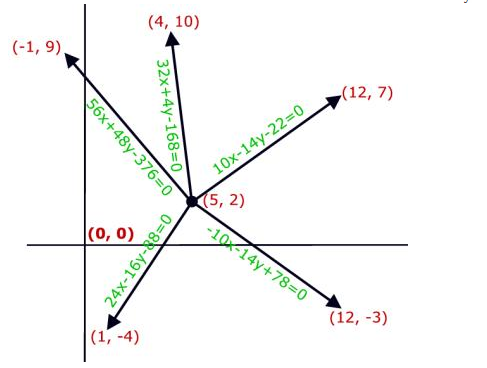
formed using the + sign. The image below shows an image where n=5, Cx=5
and Cy=2. This image corresponds to the only sample input.
|
|
|||
|
Figure: Five lines above create 5(5-1)/2=10 angles and
these angles has 10 bisectors. Of these 10 bisectors, the equation of only 4 are
formed using the + sign of the formula |
Input Format
The input file contains maximum 35 sets of inputs. The description of each set is given below:
First line of each set contains three integers C
10000). Each of the next n lines
contains two integers xi, yi (20000 ≤ xi, yi ≤ 20000) and a string
of the form aix+b
(Cx, Cy) and the string denotes the equation of the line segment formed by
connecting (Cx, C
that (-100000 ≤ ai,
bi ≤ 100000)
and (-2000000000 ≤ ci
≤ 2000000000). This equation will actually be used to find the equations
of bisectors of the angles that this line creates.
Input is terminated by a set where the value of n is zero.
Output Format
For each set of input produce one line of output. This line contains an integer number P that denotes of the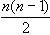 
bisector equations how many are formed using the + sign in the bisector equation 
.
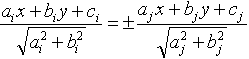Sample Input 1
5 2 5 12 7 10x-14y-22=0 1 -4 24x-16y-88=0 4 10 32x+4y-168=0 -1 9 56x+48y-376=0 12 -3 -10x-14y+78=0 10 10 0
Sample Output 1
4
Hints
Problem Source
Migrated from old NTUJ.
uva11819
Subtasks
| No. | Testdata Range | Score |
|---|