You may have solved linear equation early in the school. Problems involving
solving sets of linear equation are very important in the field of Engineering
and Mathematics.

Let us consider that we have a system of linear equations

                
a₁₁x₁ + a₁₂x₂ + a₁₃x₃
= c₁

                
a₂₁x₁ + a₂₂x₂ + a₂₃x₃
= c₂

                
a₃₁x₁ + a₃₂x₂ + a₃₃x₃
= c₃

We can solve it by reducing technique:

           
Step 1:

           
x₁ + a₁₂/a₁₁x₂ + a₁₃/a₁₁x₃
= c₁/a₁₁

           
a₂₁x₁ + a₂₂x₂ + a₂₃x₃
= c₂

           
a₃₁x₁ + a₃₂x₂ + a₃₃x₃
= c₃

            Step
2:

           
x₁ + a₁₂/a₁₁x₂ + a₁₃/a₁₁x₃
= c₁/a₁₁

                   
(-a₂₁* a₁₂/a₁₁)a₂₂x₂
+  (-a₂₁* a₁₃/a₁₁)a₂₃x₃
=  (-a₂₁* c₁/a₁₁)c₂

                   
(-a₃₁* a₁₂/a₁₁)a₂₂x₂
+  (-a₃₁* a₁₃/a₁₁)a₂₃x₃
=  (-a₃₁* c₁/a₁₁)c₂

Now do as step 1 for second row and so on.

This can be made more effective using matrix method. The set of equation
for `n' unknowns can be written as

                
a₁₁x₁ + a₁₂x₂ + a₁₃x₃
+ ... + a_1nx_n = c₁

                
a₂₁x₁ + a₂₂x₂ + a₂₃x₃
+ ... +  a_2nx_n = c₂

                
a₃₁x₁ + a₃₂x₂ + a₃₃x₃
+ ... +  a_3nx_n  = c<sub>3

                        
...   ...   ...   ...   ...  
...   ...   ...   ...   ...  
...   ...   ...   ...</sub>

                
a_m1x₁ + a_m2x₂ + a_m3x₃
+ ... +  a_mnx_n  = c_n

In matrix form



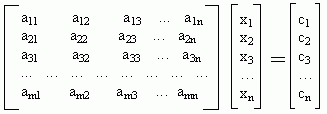
Compactly        [A] * {X} = {C}

From this we can solve values of X's. The matrix [AC] is called an
augmented (see example below) matrix. If after elimination process the
rank of matrix [A] and rank of matrix [AC] not equals, the system is called
inconsistent and it does not have a solution. If the matrix is consistent
and number of unknowns is greater then rank of matrix then the matrix system
has arbitarily many solutions containing (NumberOfUnknowns-rank) arbitary
constants. Rank of a matrix is defined as the number of non zero rows of
a matrix system. Otherwise if the rank and number of unknows equals then
the system has been solved.

For example let a system of equations be

                 
9x₁ + 4x₂ + x₃ = -17

                 
x₁ - 2x₂ - 6x₃ = 14

                 
x₁ + 6x₂  = 4

This sets of equation can be written as

9    4      1   -17

1  -2   -6      14

1    6      0       
4

So the steps involving the solution is

Step : 1

             
1            
-2            
-6            
14

             
1             
6             
0             
4

             
9             
4             
1            -17

Step : 2

             
1            
-2            
-6            
14

             
0             
8             
6            -10

             
0            
22            
55           -143

Step : 3

             
1            
-2            
-6            
14

             
0             
1             
3/4            
-5/4

             
0             
0            
77/2           -231/2

Step : 4

             
1            
-2            
-6            
14

             
0             
1             
3/4            
-5/4

             
0             
0             
1            
-3

Step : 5

             
1            
-2             
0            
-4

             
0             
1             
0             
1

             
0             
0             
1            
-3

Step : 6

             
1             
0             
0            
-2

             
0             
1             
0             
1

             
0             
0             
1            
-3

x₁ = -2

x₂ = 1

x₃ = -3

Again consider this system

        2x₁ + 2x₂
+ 2x₃ = 2

        4x₁ + 4x₂
+ 4x₃ = 4

        16x₁ + 16x₂
+ 16x₃ = 16

Steps are:

Step : 1

             
2             
2             
2             
2

             
4             
4             
4             
4

            
16            
16            
16            
16

Step : 2

             
1             
1             
1             
1

             
0             
0             
0             
0

             
0             
0             
0             
0

This system has number of unknowns 3 and rank is 1. So this system
has arbitarily many solutions containing (3-1) = 2 arbitary constants.

Another system

x + y = 10

x + y = 20

x + y = 50

Steps are:

Step : 1

             
1             
1            
10

             
1             
1            
20

             
2             
2            
50

Step : 2

             
1             
1            
10

             
0             
0            
10

             
0             
0            
30

Step : 3

             
1             
1            
10

             
0             
0            
10

             
0             
0            
30

Step : 4

             
1             
1            
10

             
0             
0            
10

             
0             
0             
1

Step : 5

             
1             
1             
0

             
0             
0             
0

             
0             
0             
1

Step : 6

             
1             
1             
0

             
0             
0             
0

             
0             
0             
1

As rank of A is not equal to the rank of augmented
matrix AC , the system has no solution.

However though there are other methods to compute this solution for
the matrix system, the main problem occurs are

        1. Round off errors or computational
error due to the use of floating point number

        2. Error due to wrong order
of the given equation.

To prevent round off error due to floating point number an approach
can be used, similar to the process of doing fractional number. So we may
use 1/3 as a expression of two integer, the numerator and the denominator,
instead of .333333 (with loss of precision). Thus we can prevent this kind
of error.

Consider this set of equations

                 
5x₃ = 10

                 
3x₂ - 3x₃ = 3

                 
2x₁ - x₂ + 2x₃ = 7

This set of equations can be written as

0     0     5   
10

0     3   -3    
3

2   -1     2    
7

Now how will you evaluate this matrix without ordering?