Solving linear Diophantine equations with three variables is not the easiest thing in the world and in this problem you will have to do something similar to that. In this problem we will deal with a specific Diophantine equation 1073x + 1827y + 3108z = 270396. Of course this equation has infinite number of all integer (The values of x, y and z are all integers) solutions, so it is pointless to ask the number of solutions. So you will have to find special type of all integer solutions.

You will be given three different possible all integer solution triples of this equation. Many other solutions can be found by taking weighted average of any two of these integer solutions (Not necessarily these newly found solutions are integer solutions). And these new solutions can be used with the given three solutions to find many other solutions by taking weighted average of any two. Your job is to find the total number of all integer solution triples obtainable in this way.

For example suppose the given
three possible solutions are (r1_x,
r1_y, r1 _{style='mso-bidi-font-size:12.0pt'>z}), (r2 _{style='mso-bidi-font-size:12.0pt'>x}, r2 _{style='mso-bidi-font-size:12.0pt'>y}, r2 _{style='mso-bidi-font-size:12.0pt'>z}) and (r3 _{style='mso-bidi-font-size:12.0pt'>x}, r3 _{style='mso-bidi-font-size:12.0pt'>y}, r3 _{style='mso-bidi-font-size:12.0pt'>z}). A new solution ( class=SpellE>r_x,
r_y,
r_z)
can be found by taking the weighted average of first two of these two
solutions. That is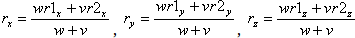

. Here (w≥0, v≥0 and (w+v)>0). Of course for
different values of w and v many solutions can be found and may be only a few
of them are all integer solutions. All the new found solutions along with the
given three solutions can be used to find infinite number of solutions by
taking the weighed average of any two. Although such solutions are infinite in
number, there are only a finite number of all integer solutions found in this
way. You are to find the total number of different all integer solutions
(triples) found.