1472 . ABCD Tiles
Description
Spring is coming! Tara is making a long list of the cleaning tasks that needs to be done as part of spring cleaning. One of the tasks is renovating the tiles of the kitchen wall.
The wall is a square of size N x N and was tiled with N x N azure tiles before few pieces fell off. Tara has ordered Soha to go out and get some azure tiles to cover those missing parts. Soha finds that the local shops have run out of azure tiles. However, they do have abundant supplies of black, crimson and drab colored tiles. These tiles aren’t the typical 1 x 1 square that we are accustomed to. Instead they are of the following shape:
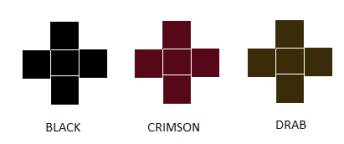
Soha bought 3000 tiles (1000 of each type).
Given the configuration of the wall, can you help them decide whether it’s possible to fill up all the empty spaces using the tiles Soha bought? For obvious reasons, a cell can’t be occupied by more than one tile. To make the tiling more beautiful, they have added another constraint – no two cells that share an edge or a corner can be filled with the tiles of the same color. This rule doesn’t apply to azure tiles, though. And of course, two cells that belong to the same tile will have the same color and so the above constraint doesn’t apply here as well. The sample input/output should make things more clear.
Input Format
The first line of input is a positive integer T (T≤1000) that indicates the number of test cases. Each case starts with an integer N (1≤N≤15). Each of the next N lines contains N characters each (giving you the configuration of the wall). Each character will either be A (meaning that cell is filled with an azure tile) or . (meaning that cell is empty).
There is a blank line before every case.
Look at the samples for more details on the format.
Output Format
For each case, output the case number first. If it’s not possible to fill up all the empty spaces using the tiles meeting the constraints mentioned, print “Not Possible!” without quotes. If it is possible, output N more lines giving the new configuration of the wall. The empty spaces should be replaced by the first letter of the color of the tile that was used to fill that cell.
Since there could be multiple solutions, choose the one that comes lexicographically earliest. Lexicographical comparisons of two configurations should be done in row major order.
Suppose we have two string arrays A and B. A will come earlier than B if for some integer x,
row(A[x]) < row(B[x]) and
row(A[i]) == row(B[i]) for i = 1 to x-1
Sample Input 1
3 3 AAA AAA AAA 5 ...AA ...AA ...AA AAAAA AAAAA 12 A.AAA.AAAA.A ...A...AA... A..AA.AAAA.A A....AAAAA.A AA....AAA... AA.A.AAAAA.A A...AAAAAAAA AA.AAAAAAAAA AAAA.AAAA.AA AAA...AA...A AAAA.AAAA.AA AAAAAAAAAAAA
Sample Output 1
Case 1: AAA AAA AAA Case 2: Not Possible! Case 3: ABAAABAAAABA BBBABBBAABBB ABCAABAAAABA ACCCDAAAAACA AACDDDAAACCC AABADAAAAACA ABBBAAAAAAAA AABAAAAAAAAA AAAABAAAABAA AAABBBAABBBA AAAABAAAABAA AAAAAAAAAAAA
Hints
Illustration of the samples:
Case 1 – There are no empty cells. That is, it’s already tiled.
Case 2 – It’s not possible to fill up all the empty cells.
Case 3 – As shown in figure.

Problem Source
Migrated from old NTUJ.
Regional Kuala Lumpur 2010
Subtasks
| No. | Testdata Range | Score |
|---|