A binary search tree is a binary tree. It may be empty. If it is not empty, it satisfies the following properties:

(1) Every node has a key, and no two nodes have the same key.

(2) The keys in a nonempty left subtree must be smaller than the key in the root of the subtree.

(3) The keys in a nonempty right subtree must be larger than the key in the root of the subtree.

(4) The left and right subtrees are also binary search trees.

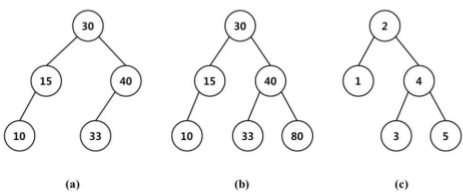
Sample binary search trees are shown in Figure 1.

To search for a node with a key k in a binary search tree T, we begin at the root. If T is empty, T contains no keys and the search is
unsuccessful. Otherwise, we compare k with the key in root. If k equals root's key, then the search terminates successfully. If k is
less than root's key, we search the left subtree of the root. If k is larger than root's key, we search the right subtree of the root.
In the same way, we can proceed the search in the left or right subree of T.

To insert a new key k into a binary search tree T where k is
different from those of existing keys in T, we first search the tree T. The search will be unsuccessful, then we insert the key at the
point the search terminated. For instance, to insert a key 80 into the Figure 1(a), we first search the tree for 80. This search terminates
unsuccessfully, and the last node examined has key 40. We insert a new node containing 80 as the right child of the node. The resulting
search tree is shown in Figure 1(b).

In this problem, we consider binary search trees with N keys <!-- MATH
$1, 2, \dots, N$
-->
1, 2,..., N. For a permutation
<!-- MATH
$a_1 \ a_2 \ \dots \ a_N$
-->
a₁ a₂ ... a_N of <!-- MATH
${1, 2, \dots, N}$
-->
{1, 2,..., N}, inserting <!-- MATH
$a_1 \ a_2 \ \dots \ a_N$
-->
a₁ a₂ ... a_N successively into an initially empty binary
search tree will produce a binary
search tree. For instance, the permutation 2 1 4 3 5 will produce the tree in Figure 1(c). Also, 2 4 3 1 5 will produce the same tree.
Actually, 8 permutations among all possible permutations of 1, 2, 3, 4, 5 will produce the same tree to the tree in Figure 1(c).

We are interested in finding the number of permutations of <!-- MATH
${1, 2, \dots, N}$
-->
{1, 2,..., N} such that all those permutations produce a binary search
tree identical to the tree produced by a given permutation P. Given N and P, you are to write a program that calculates the number of
permutations satisfying the above condition.