1491 . Sigma Function
Description
Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer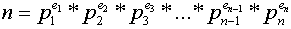 
, then 
.
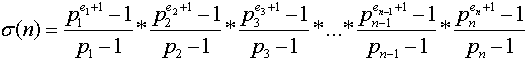For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.
Input Format
The input file contains at most 100 lines of inputs.
Each line contains an integer N (0 < N < 1000000000001).
Input is terminated by a line containing a single zero. This line should not be processed.
Output Format
For each line of input produce one line of output. This line denotes how many numbers between 1 and N (inclusive) has even value of function σ.
Sample Input 1
3 10 1000 0
Sample Output 1
1 5 947
Hints
Problem Source
Migrated from old NTUJ.
UVa 11395
Subtasks
| No. | Testdata Range | Score |
|---|