1509 . Digital Matrix
Description
You are given two N x N square matrices, A and B. Each of the elements of these matrices is an integer between 1 and K(inclusive). You have to convert matrix A into matrix B in minimum number of operations. In each operation you can choose one element of matrix A and change it to any integer between 1 and K (inclusive).
You have to ensure that after any operation the matrix is not converted to a symmetric matrix. A square matrix is said to be symmetric if j-th element of i-th row is equal to the i-th element of j-th row for all (i, j) where 1iN and 1jN. For example -
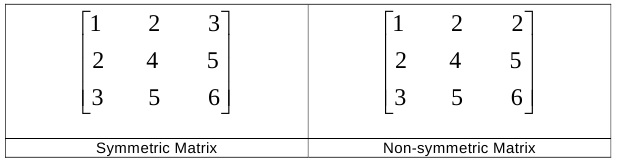
Input Format
Input will start with an integer T (T<=200), number of test cases. Each test case starts with a line containing two integers N (1<=N<=100) and K (1<=K<=9). This line will be followed by 2N lines. First N lines will represent matrix A and next N line will represent matrix B. Each of these 2N lines will contain N integers, all of these integers are in between 1 and K (inclusive).
Output Format
For each test case, output a single line containing the case number followed by the minimum number of operations required to convert A into B. If it is impossible to convert A into B obeying the rules, print `-1' instead. See output for sample input for exact formatting.
Warning: Don't use cin, cout for this problem, use faster i/o methods e.g scanf, printf.
Sample Input 1
3 3 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 2 3 1 2 1 1 1 1 3 1 2 3 1 2 3 1 1 3 2 1
Sample Output 1
Case 1: 0 Case 2: 2 Case 3: 3
Hints
Problem Source
Migrated from old NTUJ.
Regional Dhaka 2010
Subtasks
| No. | Testdata Range | Score |
|---|