1722 . Pizza Hut
TopCoder
Description
The PDF version of this problem can be downloaded here.
Every one knows the Pizza Hut, but seldom knows its special offer of composite pizzas.
A composite pizza is a square pizza with n rows and n columns, and each cell consists
of a small pizza. The customers may choose n kinds of sauces and n kinds of toppings,
and then they will get one composite pizza with n x n small pizzas of all pairs of sauce
and topping.
One day, Tomato the Great makes an extraordinary order of a 3 x 3 composite
pizza. The three sauces he chooses are tomato sauce, cream sauce, and pesto sauce.
And the three kinds of toppings he chooses are pineapple, mushroom, and sausage.
Furthermore, he would like at least one of the small pizzas with tomato sauce to be on
the first row of the composite pizza, the one with sausage topping and cream sauce to
be on the main diagonal, and none of the ones with pineapple toppings to be on the
left-most column or the last row.
The constraints are too complicated for the cook to make such composite pizza.
He does not even know if all the constraints can be satised at the same time. Thus
he turns to your help. Please write a program to check if all the constraints can be
satised, and if so, please tell the cook how to make such composite pizza.
Input Format
The first line of the input le contains an integer T (1 ≤ T ≤ 20) indicating the number of test cases.
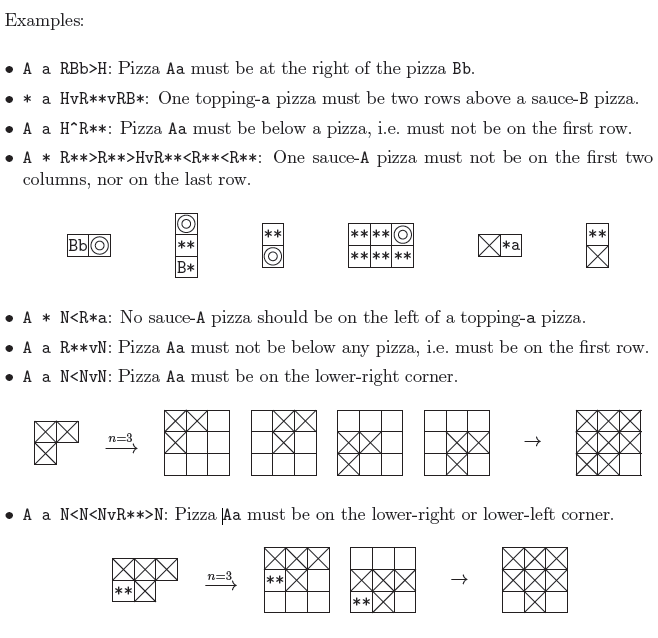
The first line of each test case contains two integers, n and m (1 ≤ n ≤ 3, 0 ≤ m ≤ n2). Then m lines follow; each describes one constraint. Each constraint contains three parts, separated by a white space: sauce type, topping type, and grid pattern. To satisfy the constraint, the small pizza with the given sauce type and topping type must be placed according to the grid pattern. The first n uppercase letters (ABC... ) indicate n types of sauce, and the first n lowercase letters (abc ... ) indicate n types of topping. An asterisk (*) in sauce type and/or topping type stands for wildcard.
Each grid pattern consists of a number of cell specications and the positional
relationship between them in the following format:
There are three types of cell specications: must-be-here (H), must-not-be-here (N), and reference (R). The reference cell specication is followed by a sauce type and a topping
type (wildcards may also be used here). There are four types of positional relationships,
up (), down (v), left (<), and right (>), indicating that the following cell is in which
direction from the previous cell.
There are two kinds of grid patterns: positive patterns and negative patterns. A positive pattern contains exactly one must-be-here cell and one or more reference cells. The constraint is satised if such positive pattern presents in the composite pizza, i.e.. the small pizza with the given sauce and topping type is placed at the must-be-here cell
with respect to the reference cells. If the given sauce or topping type or the reference
cells contain wildcards, the wildcards can be replaced with any symbol for that type.
There is at most one reference cell contains non-wildcard symbols.
A negative pattern contains at least one must-not-be-here cells, and zero or more reference cells. The constraint is satised if no such negative pattern shows up in the
composite pizza. That is, the given small pizza must not be in any must-not-be-here
cell, with respect to the reference cells (if any). (See the examples below.) There is at
most one reference cell contains non-wildcard symbol for sauce or topping type.
The input guarantees that each pattern contains at most one cell specication for
the same position.
Output Format
For each test case, please output the lexicographically smallest composite pizza satisfying all the constraint, or "IMPOSSIBLE"(without quote) if there is no solution. The composite pizza
should be printed in n lines. Each line should contain n pizza specications, separated
by a white space. Each pizza specication consists of two characters, one for sauce, and
the other for topping.
Sample Input 1
3 9
A a H>R**>R**vR**vR**
A b R**>R**vR**
A c NvR**vN>R**>N^R**
B a R**vHvR**>R**>R**
B b R**^R**^H
C a R**>R**>NvN
C b R**
3 8
A a H>R**vR**>R**vR**
B a H>R**>R**vR**
A b H^RCa
B b RAb^R**>H
C b RBb^H
A c H^R**^RCb
B c HvR**>R**vRAc
Sample Output 1
Ba Ab Ac
Cc Cb Bc
Aa Bc Cb
Ba Ca Bb
Cc Ab Ac
Hints
Problem Source
Migrated from old NTUJ.
tmt514
Subtasks
| No. | Testdata Range | Score |
|---|