223 . Cactus Reloaded
Description
Cactus is a connected undirected graph in which every edge lies on at most one simple cycle. Intuitively
cactus is a generalization of a tree where some cycles are allowed. Your task is to find a diameter of the
given cactus. Diameter is the maximal length of the shortest path between pairs of vertices.
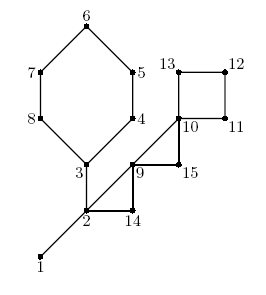
For example, on the picture above the shortest path between vertices 6 and 12 goes through 8 edges and
it is the maximal shortest path in this graph, thus its diameter is 8.
Input Format
The first line of the input file contains two integer numbers n and m (1 <= n <= 50 000, 0 <= m <= 10000).
Here n is the number of vertices in the graph. Vertices are numbered from 1 to n. Edges of the graph
are represented by a set of edge-distinct paths, where m is the number of such paths.
Each of the following m lines contains a path in the graph. A path starts with an integer number ki
(2 <= ki <= 1000) followed by ki integers from 1 to n. These ki integers represent vertices of a path.
Adjacent vertices in a path are distinct. Path can go to the same vertex multiple times, but every edge
is traversed exactly once in the whole input file. There are no multiedges in the graph (there is at most
one edge between any two vertices).
The graph in the input file is a cactus.
Output Format
Write to the output file a single integer number — the diameter of the given cactus.
Sample Input 1
15 3 9 1 2 3 4 5 6 7 8 3 7 2 9 10 11 12 13 10 5 2 14 9 15 10
Sample Output 1
8
Hints
Problem Source
Migrated from old NTUJ.
Subtasks
| No. | Testdata Range | Score |
|---|