325 . Parallelepiped walk
Description
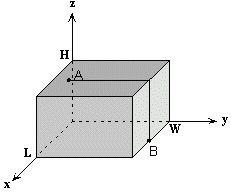
Two points A(x1, y1, z1) and B(x2, y2, z2) are placed on the surface of parallelepiped P = {(x, y, z): 0 <= x <= L, 0 <= y <= W, 0 <= z <= H} with L*W*H dimensions (see figure). These two points can be linked with various curves lying on the surface of P. You are to find out the square of the shortest curve length.
Parallelepiped dimensions L, W, H and coordinates of the points are integers, 0 <= L,W,H <= 1000.
Input Format
Input contains several test cases. Each test case contains a line with numbers (in indicated order): L, W, H, x1, y1, z1, x2, y2, z2. The numbers are separated with spaces and end-of-line characters.
Output Format
For each test case output should contain the square of the shortest curve length between points A and B on the surface of P.
Sample Input 1
5 4 2 2 0 0 2 4 2 600 300 900 300 0 899 0 300 300 600 300 900 600 300 0 0 0 0
Sample Output 1
36 718801 450000
Hints
Problem Source
Migrated from old NTUJ.
Subtasks
| No. | Testdata Range | Score |
|---|