340 . Giant Cover
Description
A student at the Lutjebroek University of Technology wants to cover all buildings of the University
with an enormous translucent plastic cover. This will make the use of umbrellas in this region
unnecessary, significantly cutting costs.
The costs of the cover are proportional to its area. With the purpose of the cover in mind, the
student wants to reduce the costs of the cover as much as possible. You are to write a program
that will help him with this by calculating the minimal area of a cover.
The whole campus terrain of the University is flat and has a rectangular shape. All buildings on
it have the shape of the union of a set of boxes, each of which stands on the ground. The cover
must cover all buildings and will be attached to the four sides of the campus at ground level.
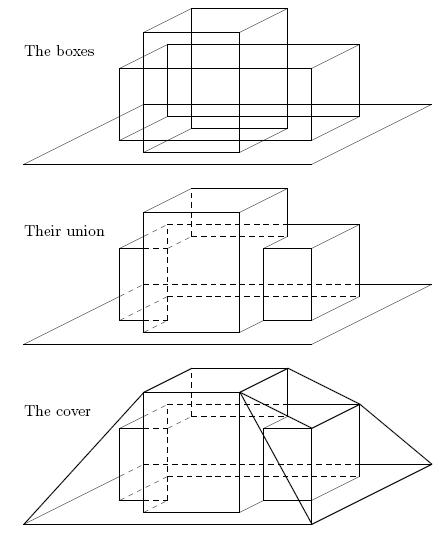
Figure 1: The last example testcase illustrated.
Input Format
The first line of the input file contains a single number: the number of test cases to follow. Each
test case has the following format:
- One line with the four integers x1, y1, x2, y2, separated by spaces, describing the campus
terrain [x1, x2]×[y1, y2]. The numbers satisfy −104 ≦ x1 < x2 ≦ 104
and −104 ≦ y1 < y2 ≦ 104.
- One line with the integer n, 0 ≦ n ≦ 400, the number of boxes that form the buildings on
the campus.
- n lines, with on the ith line the five integers ai, bi, ci, di, hi, separated by spaces, describing
a box with footprint [ai, ci] × [bi, di] and height hi above the ground. The numbers satisfy
x1 ≦ ai < ci ≦ x2, y1 ≦ bi < di ≦ y2 and 0 < hi ≦ 104.
Note: [a, c] × [b, d] is a so called Cartesian product and denotes the rectangular area
{(x, y) ∈ R2 : a ≦ x ≦ c, b ≦ y ≦ d}.
Output Format
For every test case in the input file, the output should contain a single number, on a single line:
the area of the smallest cover, using a precision of four decimals behind the decimal point. The
rounding should occur as usual; a digit is rounded up if the next digit is ≧ 5, otherwise it is
rounded down.
Sample Input 1
3 0 0 12 10 0 0 0 12 10 1 2 2 8 8 3 0 0 12 10 2 2 4 10 8 3 4 2 8 6 5
Sample Output 1
120.0000 169.7443 203.7598
Hints
Problem Source
Migrated from old NTUJ.
Subtasks
| No. | Testdata Range | Score |
|---|