The cafeteria of the EWI Faculty of Delft University of Technology has a lot of tables. These
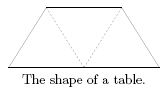
tables are not square or rectangular, they have the form of a trapezoid, an isosceles trapezoid,
with sides 1,1,1,2, as in the drawing below. It can be seen as half a hexagon or as composed of
three equilateral triangles. Such a table offers place for five to sit, though at the acute angles there
is few space for plates.



For larger companies, the tables can be put together to form a larger table. The more tables are
used, the more shapes can be created. The other way round, one may ask whether a given shape
can be built with these tables and whether that can be done in more than one way. A hexagon
can be built from two tables in three different ways.



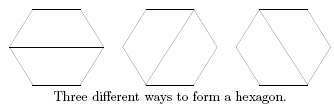
It could be argued that these three solutions may be reduced to a single solution, using rotation.
For this problem we consider these three solutions to be different, however.



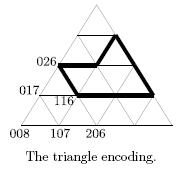
The shapes to be formed are described using a pattern of triangles. The nodes in this pattern
have a code formed from 3 digits, in the range 0 ... 8. The sum of these three digits is 8. We
describe a shape by enumerating the nodes of its contour: [116, 314, 134, 125, 026]. The contour is
built connecting the nodes along the gridlines: connect the first node with the second node, the
second node with the third one, etc., and finally connect the last node with the first. This implies
that neighboring nodes are always on a common gridline.

The following rules apply:

1. When walking along a contour, the enclosed area is on the left-hand side;


2. The enclosing contour does not cross itself, nor are nodes used multiple times;


3. The enclosed shape has no holes (in fact this is a consequence of 1 and 2).
4. 
   

A shape is given by the nodes of the enclosing contour. Calculate the number of ways this shape
can be made using the trapezoid tables.