Quadtrees are data structures used to store digital images. For our purposes, the images will be simple bitmaps, where every pixel is either a 1 (black) or a 0 (white). A quadtree representation of a bitmap is obtained as follows: first, associate the root node with the entire image. If the entire image is either all 1's or all 0's, then store that value in the node and you're done. Otherwise divide the region into four equal size quadrants, add four children to the root, and assign each child one of the four regions in the following order: the first child gets the upper left quadrant, the second the upper right, the third the lower left and the fourth the lower right. Then recursively apply the above rules to each of the children.

For example, the 4x4 image on the left would be represented by the quadtree on the right:

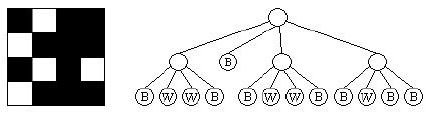
Note that this procedure only works as stated if the image is a square and has a side length equal to a power of 2. For those images which do not meet those requirements, we pad the rows and columns with 0's (on the right and on the bottom, respectively) until we have a bitmap of the appropriate size.For example, a 5x13 image would be converted to a 16x16 bitmap (with the original image residing in the upper left portion, and the remainder of the image filled with 0's).

While quadtrees can result in a significant savings in space over the original image, even more savings can be achieved if we identify repeated subtrees. For example, in the tree above, the first and third subtrees of the root are identical, so we could replace the root of the third subtree with a reference to the first subtree, obtaining something that symbolically looks like the following:



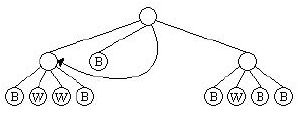
We will call these compressed quadtrees super quadtrees, or squadtrees. For our purposes the use of a reference saves space only when the tree it replaces has height of at least 1. Thus, while we could replace 5 of the nodes which contain a B with references to the first node with a B, this would not in practice save any space in the compression. Using this rule, our squadtree contains only 12 nodes, as opposed to 17 in the original quadtree. Your job for this problem is to take a set of images and determine the number of nodes in both the resulting quadtrees and squadtrees.