Plato believed what we perceive is but a shadow of reality. Recent archaeological excavations have uncovered
evidence that this belief may have been encouraged by Plato’s youthful amusement with cleverly-designed blocks.
The blocks have the curious property that, when held with any face toward a light source, they cast shadows of
various letters, numbers, shapes, and patterns. It is possible for three faces incident to a corner to correspond to
three different shadow patterns. Opposite faces, of course, cast shadows which are mirror images of one another.


The blocks are formed by gluing together small cubes to form a single, connected object. As an example, the figures
below show, layer by layer, the internal structure of a block which can cast shadows of the letters “E”, “G”, or “B”.




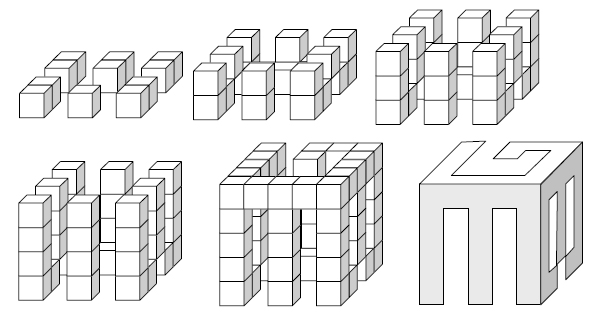
Only a partial set of blocks was discovered, but the curious scientists would like to determine what combinations of
shadows are possible. Your program, the solution to this problem, will help them! The program will input groups
of shadow patterns, and for each group will report whether or not a solid can be constructed that will cast those three
shadows.