50 . Bode Plot
Description
Consider the AC circuit below. We will assume that the circuit is in steady-state. Thus, the voltage at nodes 1 and 2
are given by v1 = VS cos ω t and v2 = VR cos ( ω t + θ ) where VS is the voltage of the source, ω is the frequency (in
radians per second), and t is time. VR is the magnitude of the voltage drop across the resistor, and θ is its phase.
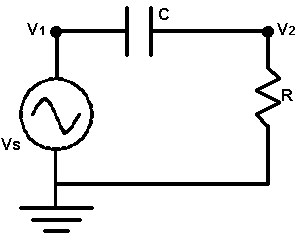
You are to write a program to determine VR for different values of ω. You will need two laws of electricity to solve
this problem. The first is Ohm’s Law, which states v2 = i R where i is the current in the circuit, oriented clockwise.
The second is i = C d/dt (v1 – v2) which relates the current to the voltage on either side of the capacitor. “d/dt”
indicates the derivative with respect to t.
Input Format
The input will consist of one or more lines. The first line contains three real numbers and a non-negative integer.
The real numbers are VS, R, and C, in that order. The integer, n, is the number of test cases. The following n lines of
the input will have one real number per line. Each of these numbers is the angular frequency, ω.
Output Format
For each angular frequency in the input you are to output its corresponding VR on a single line. Each VR value
output should be rounded to three digits after the decimal point.
Sample Input 1
1.0 1.0 1.0 9 0.01 0.031623 0.1 0.31623 1.0 3.1623 10.0 31.623 100.0
Sample Output 1
0.010 0.032 0.100 0.302 0.707 0.953 0.995 1.000 1.000
Hints
Problem Source
Migrated from old NTUJ.
Greater New York 2001
Subtasks
| No. | Testdata Range | Score |
|---|