563 . Backup
Description
You run an IT company that backs up computer data for large offices. Backing up data is not
fun, and so you design your system so that the different offices can back up each others' data while
you sit at home and play computer games instead.
The offices are all situated along a single street. You decide to pair up the offices, and for each
pair of offices you run a network cable between the two buildings so that they can back up each
others' data.
However, network cables are expensive. Your local telecommunications company will only give
you k network cables, which means you can only arrange backups for k pairs of offices (2k offices in
total). No office may belong to more than one pair (that is, these 2k offices must all be different).
Furthermore, the telecommunications company charges by the kilometre. This means that you
need to choose these k pairs of offices so that you use as little cable as possible. In other words,
you need to choose the pairs so that, when the distances between the two offices in each pair are
added together, the total distance is as small as possible.
As an example, suppose you had five clients with offices on a street as illustrated below. These
offices are situated 1 km, 3 km, 4 km, 6 km and 12 km from the beginning of the street. The
telecommunications company will only provide you with k = 2 cables.
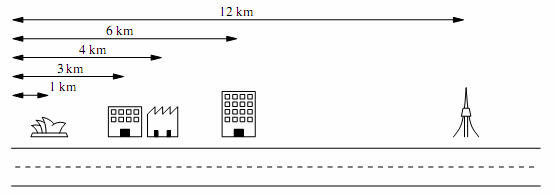
The best pairing in this example is created by linking the first and second offices together, and
linking the third and fourth offices together. This uses k = 2 cables as required, where the first
cable has length 3 km - 1 km = 2 km, and the second cable has length 6 km - 4 km = 2 km. This
pairing requires a total of 4 km of network cables, which is the smallest total possible.
Input Format
There are multiple test cases in the input file, terminated by EOF. For each test case, The first line of input will contain the integers n and k, representing the number of offices on the street (2 <= n <= 100 000) and the number of available network cables (1 <= k <= n/2)
The following n lines will each contain a single integer (0 <= s <= 1000000000), representing the
distance of each office from the beginning of the street. These integers will appear in sorted order
from smallest to largest. No two offices will share the same location.
Output Format
For each test case, the output should consist of a single positive integer, giving the smallest total length of network cable
required to join 2k distinct offices into k pairs.
Sample Input 1
5 2 1 3 4 6 12 2 1 1 3
Sample Output 1
4 2
Hints
The sample input above represents the example scenario described earlier.
Problem Source
Migrated from old NTUJ.
APIO'07
Subtasks
| No. | Testdata Range | Score |
|---|