568 . Algorithm speedup
Description
As a punishment for misbehaving, Byteasar is to calculate a certain mysterious and nasty Boolean-valued
function F(x, y), which is defined for a pair of positive integer sequences x = (x1, ..., xn), y = (y1, ..., ym) as
follows:
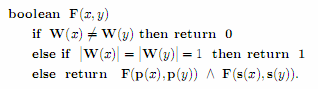
Where:
- W(x) denotes the set of members of the sequence x (order and repetitions of elements are insignificant),
- p(x) denotes the longest prefix (initial part of any length) of the sequence x, such that W(x)≠W(p(x)),
- s(x) denotes the longest suffix (final part of any length) of the sequence x, such that W(x) ≠W(s(x)),
- ∧ denotes the logical conjunction, 1 — true, 0 — false, and |Z| — cardinality of set Z.
For example, for the sequence x = (2, 3, 7, 2, 7, 4, 7, 2, 4) we have:
W(x) = {2, 3, 4, 7}, p(x) = (2, 3, 7, 2, 7), s(x) = (7, 2, 7, 4, 7, 2, 4).
For very large data a programme calculating values of the function F directly from definition is too slow by
any standards. Therefore you are to make these calculations as fast as possible.
Write a programme that reads several pairs of sequences (x, y) from the standard input and prints out the
values F(x, y) on the standard output for every input pair.
Input Format
For each test case:
The first line of the standard input contains one integer k (1 ≦ k ≦ 13) denoting the number of sequence pairs
to analyse. Next 3k line hold descriptions of test cases. The first line of each description contains two integers
n and m (1 ≦ n,m ≦ 100 000) separated by a single space and denoting the lengths of the first and second
sequence, respectively. The second line holds n integers xi (1 ≦ xi ≦ 100) that form the sequence x, separated
by single spaces. The third line holds m integers yi (1 ≦ yi ≦ 100), that form the sequence y, separated by
single spaces.
Output Format
For each test case:
The output should consist of exactly k lines; the i-th line (for 1 ≦ i ≦ k) should contain a single integer — 0
or 1 — the value of F(x, y) for i-th test case.
Sample Input 1
2 4 5 3 1 2 1 1 3 1 2 1 7 7 1 1 2 1 2 1 3 1 1 2 1 3 1 3
Sample Output 1
0 1
Hints
Problem Source
Migrated from old NTUJ.
POI 16th Stage I
Subtasks
| No. | Testdata Range | Score |
|---|