625 . Full Connectivity
Description
Full connectivity of network of roads in a new developing industrial city does not exist.
Due to existing partial connectivity it is not always possible to reach a location on a road from
another location on another road. It is considered desirable to connect all unconnected
existing network of roads with minimum cost. You are required to write a program to
determine the total minimum cost required for connecting all unconnected roads.
At the time of development of each sector, axes parallel roads are constructed in the
sector, parallel to either of the two mutually perpendicular axes passing through the city
center. The x-axis extends from west to east while the y-axis extends from south to north. The
roads extending from west to east are called Streets while the roads extending from south to
north are called avenues. A pair of points with the same y-coordinate identifies the extremities
of each street. Likewise a pair of points with the same x-coordinate identifies the extremities
of each avenue. Assume for simplicity that integer coordinates represent each extremity and
the cost of construction of roads is equal, in certain unit, to the length of the road constructed.
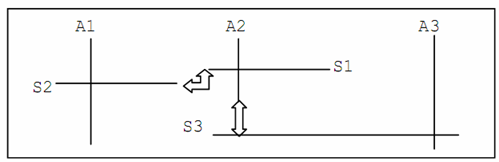
For illustration consider the connectivity of the network of roads shown in the figure
below, with three streets S1, S2, S3 and three avenues A1, A2, A3. The network is not fully
connected. However, connection with minimum cost can be established by construction of
additional roads at locations indicated by block arrows:
- Extend either S1 or S2 and join the two streets constructing a new avenue.
- Extend the avenue A2 and connect it to S3.
Input Format
Input may contain multiple test cases. Each case contains two lines.
The first line identifies all streets in an arbitrary order while the second line identifies all avenues, again in an arbitrary order. Each street is represented by three integers: the x-coordinate x0 of the extremity towards west, the x-coordinate x1 of the extremity towards east and the common y-coordinate yc. Likewise, each avenue is represented by three integers: the common x-coordinate xc, the y-coordinate y0 of the extremity towards south and the y-coordinate y1 of the extremity towards north.
Input terminates with a line containing 0 as the first input for a test case.
Output Format
For each test case, print the total minimum cost required for connecting all unconnected roads.
Sample Input 1
6 20 0 1 15 10 -9 -2 8 -7 2 10 8 3 11 19 -4 2 -6 20 10 -16 12 -6 -12 12 4 -8 -4 8 8 -12 8 0
Sample Output 1
8 2 0
Hints
Problem Source
Migrated from old NTUJ.
ICPC Kanpur, 2008
Subtasks
| No. | Testdata Range | Score |
|---|