639 . Sorted Binary Tree
Description
"Any kind of binary tree is on sale today! Cost you only two dollars. Then you can take any binary tree home if the tree is sorted as a binary search tree!"
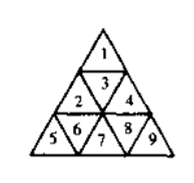
That's why you want to find a largest binary search tree on a trilateral-based pyramid. We split a equilateral triangle with side-length n into n2 little unit-length triangles. For example, the triangle of length 3 below can be split into 9 little triangles. From top to bottom and from left to right, we labeled them as 1, 2, ..., 9.
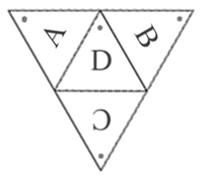
Four triangles of length n form a trilateral-based pyramid. We expand this pyramid into A, B, C, D four triangles. In the figure above, the black dot denotes the top of the triangle. We fold them into pyramid, and fill each little triangle with distinct numbers between 1 and 4n2.
Now we are going to find a largest binary search tree (which means the number of nodes is largest) on the pyramid. First we can choose an arbitrary little triangle to be the root, then pick a neighbor with smaller value to be its left child. Also pick a neighbor with larger value to be its right child.
Left children and right children are not necessary to exist for every little triangle.
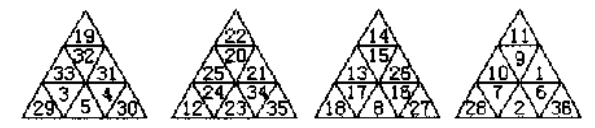
Please determine the number of nodes in this tree, and also determine the root value, left child and right child's value of the tree. If the root does not have a left child (or a right child), output -1 instead the value. If there are more than one such trees achieve maximum number of nodes, please output the lexicographically smallest answer. (We view an output to be a four-"digit" number with infinity base, a -1 is indeed smaller than other numbers.)
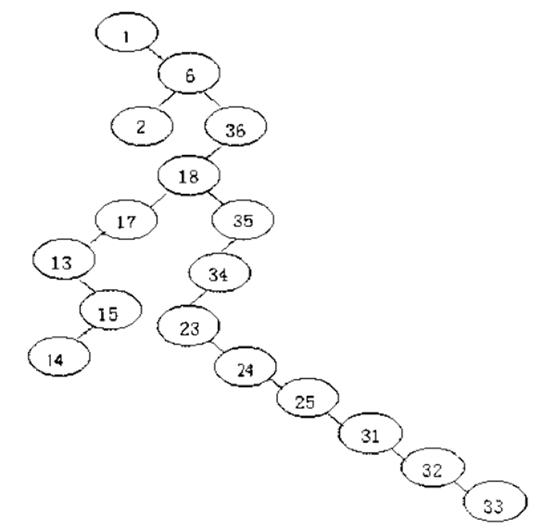
For the example figure above, we can find a largest binary search tree with 17 nodes shown below.
Input Format
There are multiple test case in the input file. For each test case, first line contain an integer n(1<=n<=20). Next 4n2 numbers seperated by one or more whitespaces or newline characters indicate the values from top to bottom, from left to right on pyramid faces A, B, C, and D respectively.
n=0 terminates the input.
Output Format
Ouptut four numbers for each test case in a line: the largest number of nodes, the root value of the tree, left child's value, and right child's value, seperated by exactly one whitespace.
Sample Input 1
3 19 33 32 31 29 3 5 4 30 22 25 20 21 12 24 23 34 35 14 13 15 26 18 17 8 16 27 11 10 9 1 28 7 2 6 36 1 2 3 4 1 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
Sample Output 1
17 1 -1 6 4 1 -1 2 15 9 5 11
Hints
Problem Source
Migrated from old NTUJ.
CTSC 2001, modified by tmt
Subtasks
| No. | Testdata Range | Score |
|---|