651 . Blast the Enemy!
Description
A new computer game has just arrived and as an active and always-in-the-scene player, you should finish it before the next university term starts. At each stage of this game, you have to shoot an enemy robot on its weakness point. The weakness point of a robot is always the ``center of mass" of its 2D shape in the screen. Fortunately, all robot shapes are simple polygons with uniform density and you can write programs to calculate exactly the center of mass for each polygon.
Let's have a more formal definition for center of mass (COM). The center of mass for a square, (also circle, and other symmetric shapes) is its center point. And, if a simple shape C
<!-- MATH
\begin{displaymath}
COM (C) = \frac{S_{A} \times COM(A) + S_{B} \times COM(B)}{S_{A} + S_{B}}.
\end{displaymath}
-->
COM(C) =
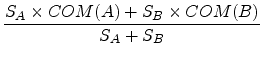 .
.
As a more formal definition, for a simple shape A
COM(A) =
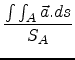
Input Format
The input contains a number of robot definitions. Each robot definition starts with a line containing n
$(n \le 100)$
-->
(n<=10,000)
* Note that the ranges are different from the origional problemset.
Output Format
The i
Sample Input 1
4 0 0 0 1 1 1 1 0 3 0 1 1 0 2 2 8 1 1 2 1 2 7 3 7 3 0 0 0 0 7 1 7 0
Sample Output 1
Stage #1: 0.500000 0.500000 Stage #2: 1.000000 1.000000 Stage #3: 1.500000 3.300000
Hints
Problem Source
Migrated from old NTUJ.
ICPC Tehran, 2008
Subtasks
| No. | Testdata Range | Score |
|---|