A plotter is a vector graphics printing device that connects to a computer to print graphical plots. There are two types of plotters: pen plotters and electrostatic plotters. Pen plotters print by moving a pen across the surface of a piece of paper. They can draw complex line art, including text, but do so very slowly because of the mechanical movement of the pens. In this problem, we are considering this matter of slowness for our special type of pen plotter. A discrete horizontal pen plotter can draw only horizontal line segments whose end points have discrete coordinates (integer x

and y
's). The drawing method is quite simple. The pen starts its journey from the upper left corner of the page (x = y = 0)
and moves only right while drawing the specified lines on that row. Then, it moves back completely to the left, moves one row down <!-- MATH
$(y \leftarrow y+1)$
-->
(y 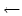y + 1)

, and repeats this task for the second row. The same is done for the next rows. In other words, the pen can move down only when it is far on the left side (i.e. when x = 0
), and can have at most one left-to-right pass and at most one right-to-left pass on each row.

It takes one unit of time to move the pen one unit of length to the left <!-- MATH
$(x \leftarrow x-1)$
-->
(x 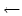x - 1)

, or to the right <!-- MATH
$(x \leftarrow x+1)$
-->
(x 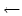x + 1)
. This time is doubled if the pen is on the paper and is drawing a line segment. It takes no time to move one row down (when x = 0
).

Since it might take a long time for the plotter to draw all the given line segments, we have decided to add a new feature to our plotter: drawing time-limit. By specifying the time-limit, the plotter should draw the maximum number of lines (using the same drawing method given above) that can be drawn within that time-limit. Given the time-limit and line segments, you should find this maximum number.