710 . Skyline
Description
It's Double Seventh Festival, and let's go to singapore for a wonderful night!

The skyline of Singapore as viewed from the Marina Promenade is one of the iconic scenes of Singapore. Country X would also like to create an iconic skyline, and it has put up a call for proposals. Each submitted proposal is a description of a proposed skyline and one of the metrics that country X will use to evaluate a proposed skyline is the amount of overlap in the proposed sky-line.
As the assistant to the chair of the skyline evaluation committee, you have been tasked with determining the amount of overlap in each proposal. Each proposal is a sequence of buildings, < b1, b2,..., bn> , where a building is specified by its left and right endpoint and its height. The buildings are specified in back to front order, in other words a building which appears later in the sequence appears in front of a building which appears earlier in the sequence.
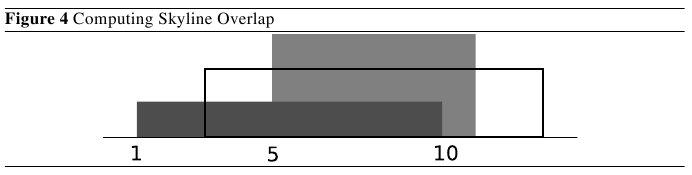
The skyline formed by the first k buildings is the union of the rectangles of the first k buildings (see Figure 4). The overlap of a building, bi , is defined as the total horizontal length of the parts of bi , whose height is greater than or equal to the skyline behind it. This is equivalent to the total horizontal length of parts of the skyline behind bi which has a height that is less than or equal to hi , where hi is the height of building bi . You may assume that initially the skyline has height zero everywhere.
Input Format
The input consists of a line containing the number c of datasets, followed by c datasets.
The first line of each dataset consists of a single positive integer, n (0 < n < 100000) , which is the number of buildings in the proposal. The following n lines of each dataset each contains a description of a single building. The i -th line is a description of building bi . Each building bi is described by three positive integers, separated by spaces, namely, li , ri and hi , where li and rj (0 < li < ri<=100000) represents the left and right end point of the building and hi represents the height of the building.
Output Format
The output consists of one line for each dataset. The c -th line contains one single integer, representing the amount of overlap in the proposal for dataset c . You may assume that the amount of overlap for each dataset is at most 5000000.
Note: In this test case, the overlap of building b1 , b2 and b3 are 6, 4 and 4 respectively. Figure 4 shows how to compute the overlap of building b3 . The grey area represents the skyline formed by b1 and b2 and the black rectangle represents b3 . As shown in the figure, the length of the skyline covered by b3 is from position 3 to position 5 and from position 11 to position 13, therefore the overlap of b3 is 4.
Sample Input 1
1 3 5 11 3 1 10 1 3 13 2
Sample Output 1
14
Hints
Problem Source
Migrated from old NTUJ.
ICPC 2007, Singapore
Subtasks
| No. | Testdata Range | Score |
|---|