712 . Parade
Description
Panagola, The Lord of city F likes to parade very much. He always inspects his city in his car and enjoys the welcome of his citizens. City F has a regular road system. It looks like a matrix with n + 1
$(n+1) \times (m+1)$
-->
(n + 1)×(m + 1)
love-hate zone". Obviously there are <span class="MATH"><i>m</i></span>welcome value" which may be negative, zero or positive. As his secretary, you must make Panagola as happy as possible. So you have to find out the best route --- of which the sum of the welcome values is maximal. You decide where to start the parade and where to end it.
<tex2html_verbatim_mark> love-hate zones in every west-east road. When passing a love-hate zone, Panagola may get happier or less happy, depending on how many people love him or hate him in that zone. So we can give every love-hate zone a
When seeing his Citizens, Panagola always waves his hands. He may get tired and need a break. So please never make Panagola travel in a same west-east road for more than k
The figure below illustrates the case in sample input. In this figure, a best route is marked by thicker lines.
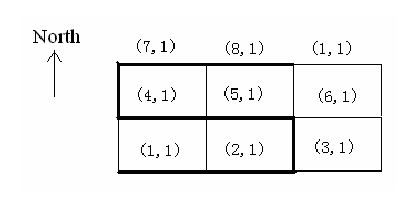
Input Format
There are multiple test cases. Input ends with a line containing three zeros.
Each test case consists of 2×n + 3 lines.
The first line contains three integers: n, m and k.(0<n<=100,0<m<=10000, 0<=k<=3000000)
The next n+1 lines stands for n + 1 west-east roads in north to south order. Each line contains m
integers showing the welcome values of the road’s m love-hate zones, in west to east order.
The last n+1 lines also stands for n + 1 west-east roads in north to south order. Each line contains
m integers showing the lengths (in minutes) of the road’s m love-hate zones, in west to east order.
Output Format
For each test case, output the sum of welcome values of the best route. The answer can be fit in a
32 bits integer.
Sample Input 1
2 3 2 7 8 1 4 5 6 1 2 3 1 1 1 1 1 1 1 1 1 0 0 0
Sample Output 1
27
Hints
Problem Source
Migrated from old NTUJ.
ICPC 2008, Beijing
Subtasks
| No. | Testdata Range | Score |
|---|