As usual, an electric power system is represented by an undirected graph G = (V, E) where V is a set of vertices containing all electric nodes of the system and E is a set of edges containing all transmission lines joining electric nodes. The power domination problem is to find a minimum placement of phase measurement units (abbreviated as PMUs) for observing whole vertices on a graph. The observation rules are as follows:

Observation Rule 1 (abbreviated as OR1):

A PMU on a vertex v observes v and all its neighbors.

Observation Rule 2 (abbreviated as OR2):

If an observed vertex u with degree d > 1 has only one unobserved neighbor v, then v becomes observed as well.

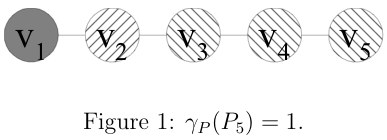
A vertex set S where PMUs are placed is a power dominating set (abbreviated as PDS) if all vertices in graph G can be observed either by OR1 initially or by OR2 recursively. The power domination number of G, denoted by γ_P(G), is the cardinality of a PDS which has the minimum number of vertices among all PDSs in G. A PDS of G with the minimum cardinality is called a γ_P(G)-set. For example, a path P₅ is shown in Figure 1. If a PMU is placed at v₁ (the gray vertex), then it observes v₁ itself and its neighbor v₂ (the slash vertex) by OR1. Next, the observed vertex v₂ has only one unobserved neighbor v₃ (a backslash vertex), then v₃ becomes observed by OR2. By the same way, v₄ and v₅ will be observed in turn. Therefore, γ_P(P₅) = 1 and the vertex set S = {v₁} is a γ_P(P₅)-set.

Let G_n,m be an n × m grid with m ≥ n ≥ 1. The vertex set V(G_n,m) = {(x, y) | 1 ≤ x ≤ n and 1 ≤ y ≤ m} and two vertices (x₁, y₁) and (x₂, y₂) are adjacent if and only if |x₁ − x₂| + |y₁ − y₂| = 1. Each vertex is labeled by x + (y − 1) ∗ n. For example, a G_7,8 is shown in Figure 2(a).

Due to the considerations of cost saving, security policy, and other factors, we consider a forbidden set F where any PMU is disallowed to place. You have to findall γ_P(G_n,m)-sets in G_n,m by considering a forbidden set F. For example, see Figure 2(b), a vertex set S = {39, 44} is a γ_P(G_7,8)-set by considering the forbidden set F = {17, 18, 19, 24, 26, 31, 33, 38, 40}. The reason is that, by OR1, vertices 32, 37, 38, 39, 40, 43, 44, 45, 46, and 51 are observed. Since vertex 45 has only one unobserved neighbor, vertex 52 becomes observed by OR2. Next, vertex 51 has only one unobserved neighbor, vertex 50 becomes observed by OR2. By using OR2 recursively, we can find that all the remaining vertices 53, 47, 54, 48, 55, 56, · · · , can be observed in turn. Consequently, the vertex set S = {39, 44} is a γ_P(G_7,8)-set. Note that vertex set S = {9, 22, 37} is also a PDS. However, it is not a γ_P(G_7,8)-set.