We would like to build a set of testing facilities on a field. Each testing takes up four units of land, and they can only be built as the following shapes.

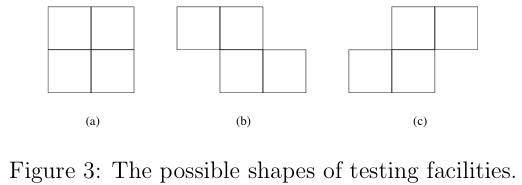
The field is an M by N rectangle. The facilities must be built according to the unit grids on the field, and the facilities cannot overlap. In addition, due to strange earth magnetic interaction, the facilities with shape (b) and (c) must be built on three columns that starts and ends at even columns. Here we assume that the grid cell at left-bottom is at column 0 and row 0, which can be represented as (0, 0), with column number appearing first. However, there is no restriction on the rows, so the facilities can be built on any rows. For example, you can build a facility with shape (c) and with grid cells at (0, 1), (1, 1), (1, 2), and (2, 2), but you cannot build a facility at (1, 0), (2, 0), (2, 1), and (3, 1), as indicated in the next figure. There is no restriction on the facilities built with shape (a).

Unfortunately not every grid cell in the field is suitable for building the testing facilities. Now given a map of the status of the cells of the field, write a program to calculate the maximum number of testing facilities that can be built at this site.

Technical Specification

1. The number of test cases is no more than 10.
2. The dimension of filed – M, and N, are both less than or equal to 200.