847 . An Interesting Problem
Description
In graph theory, tree is one of the most important kinds of graph. It can give birth to a lot of problems such as dynamic programming on a tree, minimum spanning tree, diameter of a tree and so on. And it's very interesting to solve a problem related to a tree. But today we are not going to talk about that.
As everyone knows, Edelweiss is interested in graph theory very much. Recently, he discovered a new kind of graph called cactus. First, let me give you a brief introduction to it. Cactus is a connected undirected graph in which every edge lies on at most one simple cycle. Sometimes it looks like a tree, but it may actually contain cycles just as it is defined. An important property of cactus is that it can have a number of spanning subgraphs that are also cactuses. The number of such subgraphs (including the graph itself) determines cactusness of a graph. Here is a picture for you to help understand it.
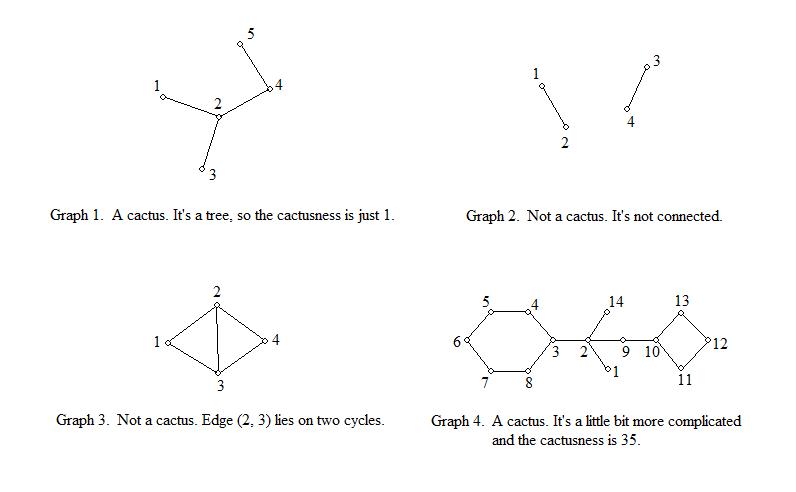
Interesting, right? Now Edelweiss wants to know the cactusness of a certain graph. But he is a lazy boy, you know. So he asks you for help: Given an undirected graph, you should first determine whether it is a cactus or not. If it is, you should calculate its cactusness. Otherwise, you just need to output a zero.
Input Format
Input contains multiple test cases. For each case, The first line contains two integers N and M (1 <= N <= 20000, 0 <= M <= 1000) where N is the number of vertices and M is the number of paths. Vertices are numbered from 1 to N. Each of the following M lines describes a path. Each line starts with an integer ki(2 <= ki <= 1000) followed by ki integers from 1 to N. These ki integers represent vertices of a path. Path can go to the same vertex multiple times, but every edge is traversed exactly once in all the paths. You are guaranteed that there is no self-loop or multiple-edge in all the graphs, i.e. no vertex will be connected with itself and no two vertices will be connected by more than one edge.
There is a blank line after each test cases. The first sample is the case for Graph 4 in the above picture.
Output Format
For each case, you should output one line containing an integer - the cactusness of the given graph. Note that cactusness can be quite a large number!
Sample Input 1
14 3 9 1 2 3 4 5 6 7 8 3 7 2 9 10 11 12 13 10 2 2 14 10 2 7 1 2 3 4 5 6 1 6 3 7 8 9 10 2
Sample Output 1
35 0
Hints
Huge input, scanf/printf is recommended.
Problem Source
Migrated from old NTUJ.
HCPC 2009 Spring
Subtasks
| No. | Testdata Range | Score |
|---|