A telecom company is developing a GSM network in the city of Beijing.
There are n houses in the city that need to be covered by the network. Due
to budget constraints, the company can install only a single antenna.

To simplify the placement of this antenna, the location will be determined
by picking 3 of the n houses to make a circle and then placing the antenna at
the center of this circle. The range of the antenna will be such that all houses
that lie within this circle, including those on the boundary of the circle, are covered.

The company plans to pick the 3 houses at random, so they want to compute the average number of houses that will be covered across all possible choices for the location of the antenna.
For example, suppose there are 4 houses, A, B, C and D located as shown in the figure below.

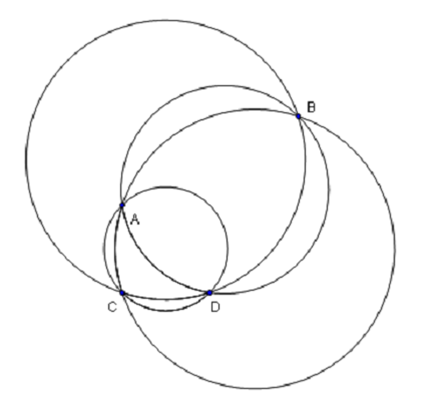
If we choose the circle defined by ABC or BCD, every house is covered.
If we choose the circle defined by ACD or ABD, the fourth house is not
within the circle covered by the antenna. Therefore, the average number of
houses covered is (1/4)*(4 + 4 + 3 + 3) = 3.5.

Your task is to compute the average number of houses covered by the
signal, given the locations of the houses. The positions of the houses are
given in terms of a 2-dimensional coordinate system in which all houses have
integer coordinates. You are guaranteed that no three houses lie on the same
line and no four of them lie on the same circle.